この記事では27卒や28卒向けにWEBテストの定番試験であるSPIの順列・組み合わせ(場合の数)問題のコツや違い、公式や例題・練習問題や過去問(頻出問題)を問題集として無料公開していきます。
SPIの順列・組み合わせは非言語問題で出題される問題で、場合の数とも言われます。順列・組み合わせは非言語問題の中で難易度は「中」に相当します。(中学から高校の数学レベルです。)
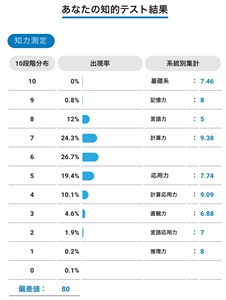
SPIの順列・組み合わせ(場合の数)の頻出問題集はこちらのアプリから行う事ができます。SPIの摸試が行えて10段階評価で行きたい企業のボーダーを超えてるか正確に自分の偏差値がわかるからおすすめです。こちらからインストールして活用してくださいね。
また、スマホでこのページを見てくださっている方限定で今まさに出題されているSPIの練習ができると評判のアプリを紹介します。
このアプリはSPIの練習だけでなく、10段階評価で自分のSPIの偏差値も出してくれて、志望企業のボーダーを突破できるのかも分かる便利アプリです。
この問題と「無料で手に入るSPIの問題集」だけやっておけばWEBテストは安心なので、スマホでこのページを見たこの機会に是非「SPIの練習ができると評判のアプリ」と「無料で手に入るSPIの問題集」を試してみてくださいね。

下記のURLからアプリインストール画面に飛べるので、今のうちにインストールして初回起動だけでもしておきましょう!
自分のSPIの出来を今のうちに判断した方が正確で対策しやすいですよ。
URLはこちら⇒https://lognavi.com/
\ 先ずはインストール /
SPI対策に時間をかけたくない場合は2月の今のうちに無料で手に入るSPIの解答集つき問題集をやっておくと就活が楽になりますよ。
▼25卒に大人気でした▼
今まさに出題されているSPIの問題があるのでチェックしておいてください。
上記の問題集は解答もあるので、正直解答集みたいなもので、あまり大声では言えませんが、26卒・27卒はこの解答を憶えれば勝てちゃいますね。
SPI問題集公式⇒https://careerpark.jp/
\ 26卒・27卒に推奨 /
それでは先ずはSPI試験の順列・組み合わせ(場合の数)のコツから解説していきます。
SPIの順列・組み合わせ(場合の数)のコツと公式を解説
それでは先ずはSPIの順列・組み合わせ(場合の数)のコツや公式から紹介します。
【順列の公式】
①n個のものを全部並べる場合
n ! = n ( n – 1 ) ( n – 2 )・・・× 1
②n個のものからr個を取り出して並べる場合
nPr = n ( n – 1 ) ( n – 2 )・・・{ n – r + 1) }
= n ! / ( n – r ) !
【円順列の公式】
n個のものを円に並べる場合
( n – 1 ) !
【組み合わせの公式】
n個のものからr個を選ぶ組み合わせの数
nCr = nPr / r !
組み合わせとは、「あるモノや人の中から何個・何人かを選び出す方法は何通りあるか?」を計算することです。
この組み合わせのコツとしては並べる順番は考慮しないのがポイントです。
それに対して順列は組み合わせと違い、並べる順番も考慮します。
順列の公式ですが、異なるn個のものの中から異なるr個を取り出し、順番も考慮して並べるときの場合の数はnPrで表すことができます。
順列・組み合わせ(場合の数)はSPI試験の非言語で出題頻度は高い
順列・組み合わせ(場合の数)はSPI試験の非言語で出題頻度は高いので、必ず正解を出せるように公式を覚えておきましょう。
公式を覚えるだけでなく、練習を繰り返す事で計算のスピードも速くなっていくので、繰り返し練習を行うのが順列・組み合わせ(場合の数)の一番のコツと言えます。
SPI試験の非言語の中でも順列・組み合わせ(場合の数)は出題頻度は高く、慣れないと難しく感じるかもしれませんが、慣れればそこまで難しい問題ではないので、とくに力を入れて早く解けるように練習する事をおすすめします。
- 今選考で出題されている問題が出る!「Lognavi」
「Lognavi」は今企業の選考で出題されているSPIの問題が出ると評判のアプリで、SPIの偏差値も出せるので、自分のレベルを知るためにも利用する価値があるアプリです。
Lognavi公式はこちら⇒https://lognavi.com/
- 最新のSPIを何度でも練習できる!「キャリアパーク」
「キャリアパーク」のSPIパーフェクト問題集は最新のSPIの問題が200問あり、解答や解説もついているので非常に学びになる無料の問題集です。
SPIの解答集つき問題集公式⇒https://careerpark.jp/
- 志望企業のSPIを通過できるかSPI判定もできる「キミスカ」
「キミスカ」はあなたが志望する企業のSPIのボーダーを突破できるか判定してくれる機能もあるサービスです。
キミスカ公式はこちら⇒https://kimisuka.com/
SPIの順列と組み合わせの違いについて
SPIで出題される順列と組み合わせは似ていますが、明確な違いがあります。
どこが違うのかというと、順列は組み合わせと違い、並べる順番も考慮しなくてはならないという事です。
単純にいうと順列は組み合わせよりもかなり答えの数が多くなるという事です。
組み合わせは(A、B、C)と(B、A、C)や(B、C、A)は全て同じものとみなします。
組み合わせは上記の通りなのですが、順列の場合は違います。
順列は(A、B、C)と(B、A、C)や(B、C、A)は全て異なるものとみなします。
このように組み合わせと順列は根本的な考え方が異なります。それではもう一度組み合わせと順列の公式を見てみましょう。
【組み合わせの公式】
n個のものからr個を選ぶ組み合わせの数
nCr = nPr / r !
【順列の公式】
①n個のものを全部並べる場合
n ! = n ( n – 1 ) ( n – 2 )・・・× 1
②n個のものからr個を取り出して並べる場合
nPr = n ( n – 1 ) ( n – 2 )・・・{ n – r + 1) }
= n ! / ( n – r ) !
組み合わせと順列の見分け方
組み合わせと順列は見分け方を誤ると答えが大きく異なり、無駄に考える時間が必要となるのでSPI試験にとっては大きなマイナスになってしまいます。
【組み合わせのポイント】
8人から3人を選んでチームを作る場合、何通りになるか・・・このような問題の時はただ3人を選ぶだけなので組み合わせの問題となります。
【順列のポイント】
9人から会長・副会長を選ぶと何通りになるか・・・このような問題の場合は、ただ2人を選ぶだけでなく会長と副会長を選ぶので(会長がA、副会長がB)と(会長がB、副会長がA)では同じAとBの人でも異なるので順列の計算となります。
それではこれらの組み合わせと順列の見分け方やコツなどを踏まえてこれから公開する練習問題を行ってみてくださいね。
SPIの順列・組み合わせ(場合の数)の例題や過去問(頻出問題)含む練習問題集を無料公開
SPIの特徴としてはWEBテストの場合は問題の形式はランダムに出題されるのですが、テストセンターの場合は正答率に応じて難易度が上がっていく構成で出題されます。
正答率を上げて企業が設定するボーダーを突破するためにも順列・組み合わせ(場合の数)の練習問題を少しでも多く行い、コツとパターンを掴むようにしましょう。
解答と解説もありますので、一問ずつ正解を確認して行うもよし、時間制限を求めて解答していったのちに答え合わせを行うもよし、自由に練習を行っていただけたらと思います。
それでは順列・組み合わせ(場合の数)の練習問題を公開していきます。
SPI【順列・組み合わせ(場合の数)】練習問題1
5人の生徒(A,B,C,D,E)を一列に並べるとき、Aが必ず一番前、Bが必ず一番後ろにいる並び方は何通りあるか。
A. 6
B. 12
C. 24
D. 36
E. 120
解答と解説を見る
【解答】A
【解説】Aを先頭、Bを最後尾に固定 → 残り3人を並べ替える → 3! = 6通り。
SPI【順列・組み合わせ(場合の数)】練習問題2
10人から3人を選んで並べる場合の数は?
A. 120
B. 210
C. 720
D. 840
E. 5040
解答と解説を見る
【解答】C
【解説】10人から3人を選び並べる → 順列 10P3 = 10×9×8 = 720。
SPI【順列・組み合わせ(場合の数)】練習問題3
6人の中から会長・副会長・書記を1人ずつ選ぶ方法は何通りか。
A. 36
B. 72
C. 120
D. 180
E. 216
解答と解説を見る
【解答】C
【解説】6人から3役を順に割り当てる → 6P3 = 6×5×4 = 120。
SPI【順列・組み合わせ(場合の数)】練習問題4
1,2,3,4,5 を使って重複せずに3桁の整数を作るとき、偶数は何通りあるか。
A. 24
B. 30
C. 36
D. 48
E. 60
解答と解説を見る
【解答】A
【解説】偶数なので末尾は {2,4} → 2通り。残り4つから2桁選び並べる → 4P2=12通り。合計 2×12=24通り。
SPI【順列・組み合わせ(場合の数)】練習問題5
コインを4回投げたとき、表がちょうど2回出る確率は?
A. 3/16
B. 5/16
C. 2/8
D. 7/16
E. 3/8
解答と解説を見る
【解答】E
【解説】全体:2^4=16通り。2回表の並び方:4C2=6。確率=6/16=3/8。
SPI【順列・組み合わせ(場合の数)】練習問題6
サイコロを2個投げたとき、和が7になる確率は?
A. 1/12
B. 1/9
C. 1/8
D. 1/6
E. 1/4
解答と解説を見る
【解答】D
【解説】全体:36通り。和=7は (1,6)(2,5)(3,4)(4,3)(5,2)(6,1) の6通り。確率=6/36=1/6。
SPI【順列・組み合わせ(場合の数)】練習問題7
52枚のトランプから2枚引くとき、両方ハートである確率は?
A. 1/13
B. 3/51
C. 1/17
D. 1/26
E. 1/34
解答と解説を見る
【解答】C
【解説】交換なしで2枚を引く。1枚目がハート:13/52、2枚目がハート:12/51。確率=(13/52)×(12/51)=156/2652=1/17。
別解:組合せで計算すると (13C2)/(52C2)=78/1326=1/17。
SPI【順列・組み合わせ(場合の数)】練習問題8
8人から3人を選んでチームを作る。ただし、AとBは同時に選ばれないとき、何通りか。
A. 40
B. 48
C. 50
D. 56
E. 64
解答と解説を見る
【解答】C
【解説】全体: 8C3=56。AとBを両方含む場合: 残り6人から1人選ぶ=6通り。差=56-6=50通り。
SPI【順列・組み合わせ(場合の数)】練習問題9
0,1,2,3,4 の5つの数字を使って、同じ数字を繰り返さずに4桁の整数を作る。ただし、
- 先頭の数字は0ではないこと
- 偶数であること
このとき、作れる整数は何通りか。
A. 48
B. 54
C. 60
D. 72
E. 84
解答と解説を見る
【解答】C
【解説】末尾が偶数 → {0,2,4} の3通り。
- 末尾が0の場合:残り {1,2,3,4} から先頭を選ぶ4通り、残り3桁は3! = 6通り → 4×6=24。
- 末尾が2の場合:残り {0,1,3,4} から先頭を0以外の3通り、残り3桁は3! = 6通り → 3×6=18。
- 末尾が4の場合も同様に18。
合計=24+18+18=60。
SPI【順列・組み合わせ(場合の数)】練習問題10
7人を円卓に並べるとき、区別できる並び方は何通りか。
A. 720
B. 360
C. 5040
D. 120
E. 840
解答と解説を見る
【解答】A
【解説】円順列: (n-1)! = 6! = 720。
SPI【順列・組み合わせ(場合の数)】練習問題11
9人から会長・副会長を選ぶとき、順番を区別して選ぶ方法は何通りあるか。
A. 36
B. 56
C. 64
D. 72
E. 90
解答と解説を見る
【解答】D
【解説】9人から2人を順番付きで選ぶ → 9P2 = 9×8 = 72。
SPI【順列・組み合わせ(場合の数)】練習問題12
1,2,3,4,5,6 の6つの数字を使って、3桁の整数を作るとき、同じ数字を繰り返さずにする場合偶数は何通りあるか。
A. 60
B. 72
C. 90
D. 96
E. 108
解答と解説を見る
【解答】A
【解説】末尾は {2,4,6} の3通り。残り5つから2桁を並べる → 5P2 = 20。合計 3×20=60。
SPI【順列・組み合わせ(場合の数)】練習問題13
12人から5人を選ぶ方法は何通りか。
A. 720
B. 792
C. 924
D. 1200
E. 1320
解答と解説を見る
【解答】B
【解説】12C5 = 792通り。
SPI【順列・組み合わせ(場合の数)】練習問題14
サイコロを3個投げるとき、すべての目が異なる確率は?
A. 5/9
B. 2/3
C. 5/12
D. 1/2
E. 2/9
解答と解説を見る
【解答】A
【解説】全体: 6^3=216。異なる目: 6×5×4=120。確率=120/216=5/9。
SPI【順列・組み合わせ(場合の数)】練習問題15
52枚のトランプをよく切り、1枚引いては山に戻す操作を2回行う。
少なくとも1枚がエース(A)となる確率はどれか。
A. 1/4
B. 25/169
C. 1/16
D. 27/64
E. 13/204
解答と解説を見る
【解答】B
【解説】1回の試行でエースを引く確率は 4/52 = 1/13。
「少なくとも1枚がA」= 1 −「2回ともA以外」
⇒1 − (12/13)²
⇒1 − 144/169
⇒25/169
SPI【順列・組み合わせ(場合の数)】練習問題16
7人を一列に並べる。ただし、AとBは隣同士にならない場合の並び方は何通りか。
A. 2400
B. 2880
C. 3600
D. 4320
E. 5040
解答と解説を見る
【解答】C
【解説】全体7! = 5040。AとBが隣になる場合: 6!×2=1440。差=5040-1440=3600。
SPI【順列・組み合わせ(場合の数)】練習問題17
7人の中から3人を選んで一列に並べる。ただし、特定の2人(A,B)は同時に選ばれない場合、並べ方は何通りか。
A. 60
B. 90
C. 120
D. 150
E. 180
解答と解説を見る
【解答】E
【解説】
- 全体の並べ方:7P3 = 7×6×5 = 210。
- AとBを両方含む場合:残り1人を他5人から選ぶ=5通り、並べ方は3!=6通り → 5×6=30。
- よって条件を満たすのは 210−30=180。
正答は E (180)。
SPI【順列・組み合わせ(場合の数)】練習問題18
0,1,2,3,4,5を使って、同じ数字を繰り返さずに作れる3桁の整数は何通りあるか。(先頭は0不可)
A. 100
B. 120
C. 150
D. 200
E. 300
解答と解説を見る
【解答】A
【解説】1桁目: 1〜5の5通り。2桁目: 残り5通り。3桁目: 残り4通り。合計 5×5×4=100。
SPI【順列・組み合わせ(場合の数)】練習問題19
コインを5回投げたとき、表が3回以上出る確率は?
A. 1/2
B. 5/8
C. 7/8
D. 11/16
E. 13/16
解答と解説を見る
【解答】A
【解説】全体: 2^5=32。表が3回: 5C3=10。4回: 5C4=5。5回: 1。合計=16。確率=16/32=1/2。
SPI【順列・組み合わせ(場合の数)】練習問題20
10人から4人を選び円卓に並べる場合の数は?
A. 420
B. 630
C. 720
D. 840
E. 1260
解答と解説を見る
【解答】E
【解説】選び方: 10C4=210。並べ方(円順列): (4-1)! = 6。210×6=1260。
また、本番形式のSPI試験はこちらで摸試も出来るので一度やっておく事をおすすめします。
このSPI対策摸試は無料で行えるのでWEBテスティングのSPI試験を極めるためにも試してみてくださいね。
SPIの組み合わせのコツや順列との違いを公式や練習問題を踏まえて解説まとめ
SPIの順列・組み合わせ(場合の数)のコツや違い、公式や例題、過去問(頻出問題)を含む練習問題は参考になりましたでしょうか。
今回公開している練習問題はまだ一部なので、もっと練習問題を行いたい場合は問い合わせなどから連絡をいただければ追記致します。
またこちらの記事でもSPI試験の練習問題を無料公開しているので、色々な問題を繰り返してSPIに慣れていきましょう。
SPIは練習をしっかりと行えば難しい問題ではないので、順列・組み合わせ(場合の数)を含めて練習を欠かさずに行っておきましょう。
スマホでこのページを見ている方限定でお伝えしたいのが、今まさに出題されているSPIの問題が出ると評判の「Lognavi」というアプリです。
MBTI顔負けの性格診断も出来て、あなたの市場価値まで企業側に伝わって超大手優良企業からのオファーももらえちゃうから一石二鳥です!

下記のURLからアプリインストール画面に飛べるので、今のうちにインストールして初回起動だけでもしておきましょう!
自分のSPIの出来を今のうちに判断した方が正確で対策しやすいですよ。
アプリインストールはこちらから⇒https://lognavi.com/
※インストール後の初回起動はお早めに
\ 先ずはインストール /
ESや企業研究でSPIに時間を割く暇がないと思うので、今選考で出題されているSPIの練習が無料でできるSPIの無料問題集をやっておいてください。
無料でダウンロードできるので、SPIに時間をかけたくない場合は使ってみてください。
▼25卒に大人気でした▼
参考書や問題集と違って問題が最新版にアップデートされるので、今どのような問題が出題されているのか、頻出問題ばかりなのでチェックするためにも利用すると良いでしょう。
とくにWEBテストは出題される問題の難易度もまばらなので、長文や推論などが苦手な学生ほど使っておく事をおすすめします。
一応リンク貼っておくので、自由に使ってみてください。
SPI問題集公式⇒https://careerpark.jp/
こちらの記事も参考にしてくださいね。
















コメント