この記事では27卒や28卒のためにWEBテストの定番であるSPIの非言語問題である推論のコツや解き方、例題や無料練習問題を公開していきます。
SPI非言語の推論は難しいから捨てるという学生もいるくらいなので、SPIの推論が苦手な学生は解き方をしっかりと把握して挑む必要があります。
SPI試験の非言語の推論を捨てたら、とくにテストセンターのSPIではボーダーを突破する事ができない企業も多いので、SPIの非言語は推論で終わる事を目標にして当サイトで公開している練習問題などを活用していただけたらと思います。
SPIの非言語の推論の頻出問題集はこちらのアプリから行う事ができます。SPIの摸試が行えて10段階評価で行きたい企業のボーダーを超えてるか正確に自分の偏差値がわかるからおすすめです。こちらからインストールして活用してくださいね。
また、スマホでこのページを見てくださっている方限定で今まさに出題されているSPIの練習ができると評判のアプリを紹介します。
このアプリはSPIの練習だけでなく、10段階評価で自分のSPIの偏差値も出してくれて、志望企業のボーダーを突破できるのかも分かる便利アプリです。
この問題と「無料で手に入るSPIの問題集」だけやっておけばWEBテストは安心なので、スマホでこのページを見たこの機会に是非「SPIの練習ができると評判のアプリ」と「無料で手に入るSPIの問題集」を試してみてくださいね。

下記のURLからアプリインストール画面に飛べるので、今のうちにインストールして初回起動だけでもしておきましょう!
自分のSPIの出来を今のうちに判断した方が正確で対策しやすいですよ。
URLはこちら⇒https://lognavi.com/
\ 先ずはインストール /
SPI対策に時間をかけたくない場合は2月の今のうちに無料で手に入るSPIの解答集つき問題集をやっておくと就活が楽になりますよ。
▼25卒に大人気でした▼
今まさに出題されているSPIの問題があるのでチェックしておいてください。
上記の問題集は解答もあるので、正直解答集みたいなもので、あまり大声では言えませんが、26卒・27卒はこの解答を憶えれば勝てちゃいますね。
SPI問題集公式⇒https://careerpark.jp/
\ 26卒・27卒に推奨 /
また、本番形式のSPIはこちらで摸試も出来るので一度やっておく事をおすすめします。
このSPI対策摸試は無料で行えるのでWEBテスティングのSPIを極めるためにも試してみてくださいね。
【関連記事】
- SPI非言語が推論で終わる!テストセンターで推論が何問出るのが理想か解説
- SPIテストセンターで2タブばっかり!非言語の推論で2タブはやばいのか解説
- SPIテストセンターで推論ばかり出る理由!チェックボックスが出れば7割以上期待できる?
SPI非言語の推論のコツと解き方を解説

それでは先ずはSPIの非言語の中でも難関である推論のコツと解き方から紹介していきます。
| 種類 | ポイント |
|---|---|
| 推理(位置) | 問題文を記号などに置き換える ①条件(隣接しているか、隣接していないか)を図式化して整理する ・X→Y (例)XはYには接しているがZとは接していない ・X/→Z ②接している区画数を確認する |
| 推理(順序・トーナメント) | 記号を使って順列を図形化する ・AはBより早かった A>B ・AはBより早かったが間に1人いる A>□>B ・AはBよりひとつ早かった |
| 推理(論理) | さまざまな言い回しに注意する 発言の正誤を導く出題パターンを覚える SPIの論理の問題において、さまざまな表現で出題される。 ・「確実にいえる」 ⇒すべてにおいて正しい ・「明らかに誤り」 ⇒すべてにおいて誤り ・「必ずしも正しくない」 ⇒すべてにおいて正しくない。どれか誤ったケースがある ・「必ずしも誤りでない」 ⇒すべてにおいて誤りでない。どれか正しいケースがある ・「どちらともいえない」 ⇒与えられた資料・数値からは判断できない |
SPIの推論を解くためのコツは他にもあるので、一つずつ解説していきます。
SPIの推論のコツと解き方「文章を丁寧に読み、早く理解する」
SPIの推論の問題を解くときは、問題文を丁寧に読むことが重要です。
ただ、SPIは制限時間が設けられているため、ただただ丁寧に読んでいるだけでは時間が無くなってしまうので、早く理解する事が大切です。
早く理解しなくては・・・と焦ってしまう学生もいますが、焦ると読み間違えて不正解の選択肢を選んでしまうこともあるので、問題を早く理解するために日頃から練習問題を繰り返すのが大切です。
推論は他の問題よりも制限時間が長く設定されているため、落ち着いて文章を読み、自分なりのやり方で構わないので情報を整理できるように日頃から練習を行いましょう。
SPIの推論のコツと解き方「紙に書き出して読解・整理する」
SPIの推論が苦手な学生は、問題を頭の中で考えていこうとすると、途中で混乱してしまう事が良くあります。
そこでおすすめなのが、メモを紙に書き出していくことです。考えられるパターンや条件を表・図・グラフなどに書き出すことで、情報を視覚的に整理する事が出来るので、SPIの推論が苦手な学生にかなり有効です。
頭の中でだけ考えていると、情報が抜け落ちてしまうので、紙に書きながら思考する方が視覚情報を元に考える事ができるので、ケアレスミスも減らせて正解率の向上に繋がります。
SPIの推論のコツと解き方「問題のパターンに慣れる」
SPIの問題は毎年アップデートされるとは言えど、出題内容がパターン化されているため、推論の問題も出題パターンに慣れてしまえば、攻略するのもそこまで難しい事ではありません。
- 順序
- 整数
- 割合
- 平均
- 位置
- 対戦(リーグ戦・トーナメント戦)
SPIの推論の問題は初めてを見ると戸惑うかもしれませんが、時間をかけて解き方を身につけることで、焦らず正解を導き出すことができます。
問題集を使って解き方に慣れておけば、SPIの本番でもスムーズに回答できるようになるので、先ずは繰り返し問題を解く事から始めましょう。
- 今選考で出題されている問題が出る!「Lognavi」
「Lognavi」は今企業の選考で出題されているSPIの問題が出ると評判のアプリで、SPIの偏差値も出せるので、自分のレベルを知るためにも利用する価値があるアプリです。
Lognavi公式はこちら⇒https://lognavi.com/
- 最新のSPIを何度でも練習できる!「キャリアパーク」
「キャリアパーク」のSPIパーフェクト問題集は最新のSPIの問題が200問あり、解答や解説もついているので非常に学びになる無料の問題集です。
SPIの解答集つき問題集公式⇒https://careerpark.jp/
- 志望企業のSPIを通過できるかSPI判定もできる「キミスカ」
「キミスカ」はあなたが志望する企業のSPIのボーダーを突破できるか判定してくれる機能もあるサービスです。
キミスカ公式はこちら⇒https://kimisuka.com/
SPIの推論を早く解くコツ!時間切れを防ぐ方法
SPIの非言語問題の中で、推論問題は多くの受験者が「時間が足りない」「最後まで解ききれない」と感じやすい分野です。
そのため、解き方が定まっていないと、どうしても思考が迷走し、時間を大きく消費してしまいます。
また、SPIの推論問題は一見すると文章量が多く、複雑そうに見えることが多いため、最初の段階で「難しそうだ」という心理的なブレーキがかかりやすい点も特徴です。
この心理的負荷が、読むスピードや判断の速さをさらに低下させ、結果として時間不足につながります。
推論問題を早く解くためには、単に計算スピードを上げるのではなく、「考え方そのもの」を効率化することが何より重要です。
推論問題は「全文を理解しようとしない」ことが重要
SPIの推論問題で時間がかかる最大の原因は、文章を最初から最後まで丁寧に理解しようとしてしまうことです。
早く解くためには、文章の意味を「理解」するのではなく、「条件として処理」する意識が大切です。
たとえば、「AはBよりも背が高い」「CはDよりも年上だが、Aよりは年下だ」といった文章を、頭の中でそのまま文章として捉えるのではなく、「A>B」「D<C<A」といった関係性に即座に置き換える癖をつけることが、スピードアップの第一歩になります。
文章を読んでイメージを膨らませようとすると、その分だけ時間がかかります。推論問題では、情景を思い浮かべる必要はなく、関係性だけを抜き出せれば十分です。
「整理しながら考える」のではなく「先に整理する」意識を持つ
多くの受験者は、文章を読みながら頭の中で考え、整理し、結論を出そうとします。
しかしこの方法は、情報が増えるほど混乱しやすく、途中で条件を忘れたり、行き戻りが発生したりします。これが時間ロスの大きな原因です。
推論問題を早く解くためには、「考えながら整理する」のではなく、「整理してから考える」という順序を意識することが重要です。
頭の中だけで処理しようとせず、関係図や簡単なメモを使って情報を一元化すると、判断が一気に速くなります。結果として、迷いが減り、解答までの時間が短縮されます。
図や表は「完璧に作らない」ことがスピードアップにつながる
推論問題では、人物関係、順位、大小関係などを図や表に整理する場面が多くあります。ただし、この図や表を「きれいに」「正確に」作ろうとすると、逆に時間がかかってしまいます。
SPIで求められているのは、見やすい図ではなく、「自分が判断できる最低限の情報」です。多少雑でも、自分が関係性を把握できれば十分です。
線が曲がっていても、文字が多少重なっていても、判断に支障がなければ問題ありません。
図を書く目的は、思考を省略することにあります。図を書くこと自体が目的になってしまうと、かえってスピードが落ちてしまいますので、「何を判断するために書いているのか」を常に意識することが大切です。
選択肢から逆算する意識を持つと判断が速くなる
推論問題では、すべての条件を完全に整理しきらなくても、選択肢を見れば答えが絞れるケースが多くあります。そのため、問題文を読み終えたら、すぐに選択肢に目を通すことが有効です。
選択肢を見ることで、「この問題は何を判断させたいのか」「どの関係性がポイントなのか」が明確になります。すると、不要な情報を深追いせずに済み、必要な条件だけに集中できます。
特に、「正しいものを選べ」「必ず成り立つものはどれか」といった形式では、すべての関係を完全に確定させる必要はありません。
選択肢ごとに「これは条件と矛盾しないか」「一つでも成り立たない可能性があるか」とチェックするだけで、短時間で答えにたどり着けることが多いです。
「全部解こう」としない判断力もスピードには欠かせない
SPIは制限時間が厳しく、すべての問題を完璧に解くことは想定されていません。特に推論問題は、1問に時間をかけすぎると、後半で大きく失点するリスクがあります。
推論問題は1問あたりの配点が極端に高いわけではありません。全体の正答率を意識し、取れる問題を確実に取ることが、結果的に最も効率の良い解き方になります。
普段の練習で「考え方の型」を身につけることが最大の近道
推論問題を早く解けるようになる最大のコツは、本番で頑張ることではなく、普段の練習で「考え方の型」を身につけておくことです。
練習の段階で、「このタイプはこう整理する」「この形式は図を書くと速い」といった自分なりの型を作っておくと、本番ではほとんど反射的に手が動くようになります。その結果、読む時間、考える時間、迷う時間がすべて短縮されます。
逆に、型がないまま本番を迎えると、毎問ゼロから考えることになり、どうしても時間が足りなくなってしまいます。
推論を早く解く鍵は「思考の省略」にある
SPIの非言語における推論問題を少しでも早く解くためには、計算力や頭の良さ以上に、「どれだけ思考を省略できるか」が重要です。
文章を条件として処理し、先に整理し、必要最低限の図やメモで判断し、選択肢を活用する。この一連の流れを身につけることで、推論問題にかかる時間は確実に短くなります。
また、すべてを完璧に解こうとしない判断力や、日頃から型を意識した練習を行うことも、スピードアップには欠かせません。
推論問題は慣れによって大きく差が出る分野です。考え方を整理し、無駄な思考を減らすことで、SPI非言語の推論は確実に「間に合う問題」へと変わっていきます。
SPIの推論のコツを掴むために難しい例題・練習問題を無料公開
それではここからは、SPIの推論のコツを掴むためにも非言語の練習問題を無料公開していきます。
SPI【推論のコツと解き方】難しい練習問題1
A~Dの4人がテストを受けた。次のことがわかっている。
- AはBより点数が高い。
- CはAより低い。
- DはAより高い。
最も高得点を取ったのは誰か?
A. A
B. B
C. C
D. D
E. AまたはD
F. BまたはC
解答と解き方のコツを見る
【解答】D
【解説】条件を整理すると、順位は D > A > B または C となるため、最高点はDである。
SPI【推論のコツと解き方】難しい練習問題2
4人(P, Q, R, S)がマラソンを走った。
- QはSより早い。
- RはQより遅い。
- PはSより遅く、Rより早い。
最も遅かったのは誰か?
A. P
B. Q
C. R
D. S
E. PまたはQ
F. QまたはS
解答と解き方のコツを見る
【解答】C
【解説】条件を整理すると、順位は Q > S > P >R となるため、最も遅いのはRである。
SPI【推論のコツと解き方】難しい練習問題3
4人(甲、乙、丙、丁)が総当たり戦で対戦した。
- 甲は乙に勝ったが丙に負けた。
- 丁は丙と乙に勝った。
- 丙は乙に負けた。
最も勝ち星が多いのは誰か?
A. 甲
B. 乙
C. 丙
D. 丁
E. 甲または丁
F. 乙または丙
解答と解き方のコツを見る
【解答】E
【解説】条件を整理すると、乙と丙は1勝ずつなのは確定。丁は2勝以上が確定しているが、甲と丁の結果が不明のため甲は2勝か1勝。よって正解は、甲または丁。
SPI【推論のコツと解き方】難しい練習問題4
A~Dが英語テストを受けた。
- AはCより高得点。
- DはAより低い。
- CはBより高い。
最も点数が高いのは誰か?
A. A
B. B
C. C
D. D
E. AまたはC
F. BまたはD
解答と解き方とコツを見る
【解答】A
【解説】Dがどの位置に入るか確定はできないが、AがBCDよりも点数が高いことは推測されるので、最高得点はAである。
SPI【推論のコツと解き方】難しい練習問題5
X, Y, Z, Wが短距離走に参加した。
- XはYより遅い。
- WはZより早い。
- YはWより早い。
最も早いのは誰か?
A. X
B. Y
C. Z
D. W
E. YまたはZ
F. WまたはX
解答と解き方とコツを見る
【解答】B
【解説】XがWやZとの比較がないため順位は特定できないが、YはXYZよりも早いこと早いことが推測されるため、最速はYである。
また、今まさに出題されているWEBテストの練習ができると評判のアプリを紹介します。
このアプリはWEBテストの練習だけでなく、10段階評価で自分のWEBテストの偏差値も出してくれて、志望企業のボーダーを突破できるのかも分かる便利アプリです。
この問題と「無料で手に入るWEBテストの問題集」だけやっておけばWEBテストは安心なので、スマホでこのページを見たこの機会に是非「WEBテストの練習ができると評判のアプリ」と「無料で手に入るWEBテストの問題集」を試してみてくださいね。

こちらのURLからアプリインストール画面に飛べるので、今のうちにインストールして初回起動だけでもしておきましょう!そしてWEBテストのボーダーを突破しましょう!
※PCでご覧の場合は、URLをクリック後にお手元のスマホでQRコードを読み込んでくださいね。
URLはこちら⇒https://lognavi.com/
\ 先ずはインストール /
もしWEBテストに自信が持てない場合は、選考対策をサポートしてもらえる「キャリタス就活エージェント」を利用すると良いでしょう。

「キャリタス就活エージェント」では厳選された企業、外資系企業やグローバル展開する優良企業の非公開求人なども紹介してくれるので、驚くような企業の内定も期待できますし、選考対策もサポートしてくれるので1人で悩まずに済みます。
専任のキャリアアドバイザーが応募書類や面談に対する対策もしてくれるので、1人で選考対策をするよりも、数々の企業の情報を握っているキャリアアドバイザーに頼る方が内定率の向上も望めるので、選考対策に悩みがある場合は必ず相談してみましょう!
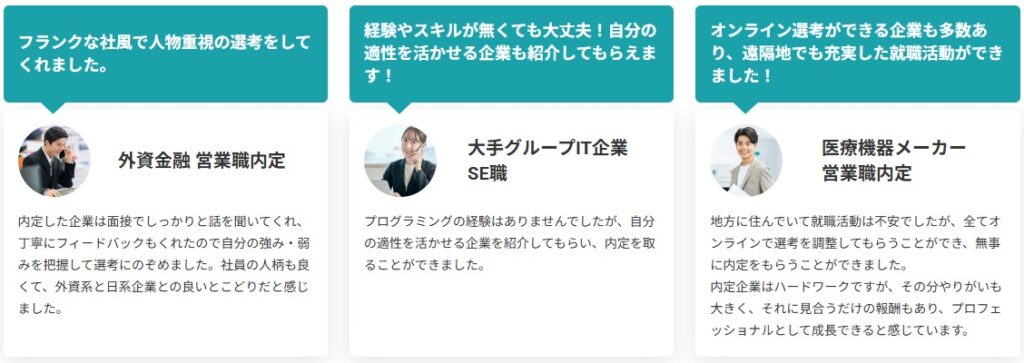
「キャリタス就活エージェント」は全て無料で完結できるので、これから内定が少しでも早く取りたい場合は是非利用してみてくださいね。
また、滑り止めとして優良企業の内定も取れるので、今のうちに登録しておきましょう。
公式ページ⇒https://agent.career-tasu.jp/
\ 登録は30秒で完了 /
SPI【推論のコツと解き方】難しい練習問題6
A, B, C, D, Eの5人が横一列に並んだ。次のことがわかっている。
- AはBより右側にいる。
- CはAの左隣にいる。
- DはEの左隣にいる。
- Eは列の一番右端にいる。
中央(3番目)にいるのは誰か?
A. A
B. B
C. C
D. D
E. E
F. AまたはC
解答と解き方とコツを見る
【解答】A
【解説】並びは B–C–A–D–E となるため、中央はAである。
SPI【推論のコツと解き方】難しい練習問題7
ある総当たり戦でP, Q, Rの3人が1回ずつ対戦した。
- PはQに勝った。
- QはRに勝った。
- RはPに負けた。
勝ち星が最も多いのは誰か?
A. P
B. Q
C. R
D. PまたはQ
E. QまたはR
F. 全員同じ
解答と解き方とコツを見る
【解答】A
【解説】対戦結果は P>Q、Q>R、P>R。Pは2勝、Qは1勝、Rは0勝でPが最多。
SPI【推論のコツと解き方】難しい練習問題8
4人(甲、乙、丙、丁)が左から右へ一列に座った。次のことがわかっている。
- 甲は丙の左隣にいる。
- 丁は丙の右隣にいる。
- 乙は丙の右側にいる。
最も右端に座っているのは誰か?
A. 甲
B. 乙
C. 丙
D. 丁
E. 甲または乙
F. 丙または丁
解答と解き方とコツを見る
【解答】B
【解説】(1)(2)より並びは [甲 丙 丁 _]。さらに(3)より乙は丙より右側に座るため [甲 丙 丁 乙] が唯一。右端は乙。
SPI【推論のコツと解き方】難しい練習問題9
A, B, Cの3人が集めた募金額の合計は30,000円である。次のことがわかっている。
- AはBの2倍集めた。
- CはBより5,000円多い。
最も多く集めたのは誰か?
A. A
B. B
C. C
D. AまたはC
E. BまたはC
F. 全員同じ
解答と解き方とコツを見る
【解答】A
【解説】B=x とすると A=2x、C=x+5,000。合計 2x + x + (x+5,000)=30,000 より 4x=25,000、x=6,250。A=12,500、C=11,250、B=6,250 でAが最多。
SPI【推論のコツと解き方】難しい練習問題10
X, Y, Zの3人がそれぞれ貯金をしている。合計は95,000円である。次のことがわかっている。
- XはYの2倍より5,000円多い。
- ZはYのちょうど3倍の金額を持っている。
最も多く貯金しているのは誰か?
A. X
B. Y
C. Z
D. XまたはZ
E. YまたはZ
F. 全員同じ
解答と解き方とコツを見る
【解答】C
【解説】Yをxとすると X=2x+5,000、Z=3x。合計 (2x+5,000)+x+3x=95,000 より 6x+5,000=95,000、6x=90,000、x=15,000。X=35,000、Y=15,000、Z=45,000 となり、最も多いのはZ。
- 今選考で出題されている問題が出る!「Lognavi」
「Lognavi」は今企業の選考で出題されているSPIの問題が出ると評判のアプリで、SPIの偏差値も出せるので、自分のレベルを知るためにも利用する価値があるアプリです。
Lognavi公式はこちら⇒https://lognavi.com/
- 最新のSPIを何度でも練習できる!「キャリアパーク」
「キャリアパーク」のSPIパーフェクト問題集は最新のSPIの問題が200問あり、解答や解説もついているので非常に学びになる無料の問題集です。
SPIの解答集つき問題集公式⇒https://careerpark.jp/
- 志望企業のSPIを通過できるかSPI判定もできる「キミスカ」
「キミスカ」はあなたが志望する企業のSPIのボーダーを突破できるか判定してくれる機能もあるサービスです。
キミスカ公式はこちら⇒https://kimisuka.com/
SPI【推論のコツと解き方】難しい練習問題11
A, B, C, Dの4人が会議に出席した。
- AかBのどちらかは必ず発言する。
- CとDは同時に発言しない。
- Dが発言した場合、必ずAも発言する。
Bが発言しなかったとき、発言したことが確定できるのは誰か?
A. A
B. B以外
C. C
D. AとD
E. AとC
F. 誰も確定できない
解答と解き方とコツを見る
【解答】A
【解説】Bが発言しない場合、条件1からAが必ず発言する。条件2によりCとDが同時に発言はできない。条件3よりDが発言すればAも発言するが、Aが発言すればDも発言するかは分からない。確定して発言しているのはAである。
また、どうしてもWEBテストを始めとする書類選考が苦手!無理!という事であれば、書類選考カットのオファーがもらえる可能性が高い「OfferBox」を利用してください。
- ESやWEBテストカットのオファーも届く
- 面接に強くなれる自己分析を無料で行える
- 就活に役立つ情報が定期的に送られてくる
上記のようなメリットがあるので、登録しておいて損はありません。
しかも大手を中心として優良企業もオファーを送信中なので、特別ルートの選考で内定まで進める事も期待できます。
↓以下企業が積極送信中↓
企業も内定枠が埋まり次第オファーを送信しなくなってしまうので、今のうちに登録しておくと良いでしょう。
OfferBox公式ページ⇒https://offerbox.jp/
SPIの非言語は推論で終わる事が高得点の目標
SPIテストセンターの非言語を行っている時に推論問題が出てきた場合、それは高得点を取れているという事です。
SPIのテスト問題の中で最も難易度が高いと言われているのが推論であり、推論の問題が多く出題されると、必然的に難易度が高い問題を与えられている事が考えられるため、SPIの非言語が推論で終わる事が高得点が取れていると判断できます。
ボーダーが高い大手企業の通過基準として、推論問題が全体の半数以上を占めている事が挙げられるくらい、高得点の指標として推論の問題数は重要なのです。
つまり、SPIテストセンターのボーダーが高い大手企業の非言語問題で簡単な問題ばかりで推論が少ない、または出題されない場合は得点があまり取れていないと思っていいです。
ボーダーが高い企業に挑戦する時こそ推論は大切
ボーダーが高い企業に挑戦する場合は、正直推論との闘いになります。
とくにテストセンターやテストセンターオンラインの場合はSPI解答集は使えないので、不正行為は完全にNGです。
高得点だと推論の解答方法が変わる
通常のSPIの推論問題は、上記練習問題のように選択肢の中から一つの答えを選ぶ形になります。
チェックボックスとは何かというと、簡単に言えば選択形式の問題の事です。
選択形式の問題というのは、「この問題の答えとして正しいものを以下の選択肢の中から全て選びなさい」というような形式で、答えが複数あるタイプのものです。
高得点を取っていると、このようにチェックボックス形式の問題が出され、正しいものを全て選択し、全て合っていないと正解にならないので理解度の高さが試されます。
高得点を取っていると非言語問題約10問のうち5問以上推論が出題される場合があるので、ここで落とさないようにこの記事で紹介しているコツをしっかりと掴み、8割や9割を目指していきましょう。
高得点を目指すためにSPIの自分の偏差値を把握したり、練習を繰り返す事が大切なので、不正を考えるよりも確実に身につくSPIの推論対策を行っていきましょう。
SPIテストセンター推論チェックボックスの例題・練習問題を無料公開
ここからはSPIのテストセンターの推論対策として、テストセンターの推論で正答率が高いと出題されるチェックボックス形式の例題・練習問題を無料公開します。
チェックボックス形式の推論問題は難易度が非常に高いので、ここで練習を行って本番に備えて頂けたらと思います。
実際にはチェックボックスで複数選択する形ですが、ここで紹介する問題はチェックボックスではなく、複数の正解がある形での例題紹介になるので、予めご了承ください。
SPIの推論【テストセンター】チェックボックス練習問題①
A、B、C、D、Eの5人が一列に並んでいる。以下の条件がわかっている。
- AはCの左にいる。
- DはEの左にいる。
- BはAの右にいる。
- CはDの右にいる。
このとき、正しい並びの可能性をすべて選びなさい。
A. A – B – D – C – E
B. A – D – B – C – E
C. A – B – C – D – E
D. A – B – E – C – D
E. A – C – B – D – E
解答と解説を見る
解答: A, B
解説:
各選択肢が条件に適合するか確認します。
- AはCの左にいる → AはCより左側
- DはEの左にいる → DはEより左側
- BはAの右にいる → BはAより右側
- CはDの右にいる → CはDより右側
| 選択肢 | 並び順 | AはCの左 | DはEの左 | BはAの右 | CはDの右 | 適合 |
| A | A – B – D – C – E | ○ | ○ | ○ | ○ | ✅ |
| B | A – D – B – C – E | ○ | ○ | ○ | ○ | ✅ |
| C | A – B – C – D – E | ○ | ○ | ○ | × | ❌ |
| D | A – B – E – C – D | ○ | × | ○ | × | ❌ |
| E | A – C – B – D – E | ○ | ○ | ○ | × | ❌ |
したがって、正解は A, Bです。
SPIの推論【テストセンター】チェックボックス練習問題②
あるレースで、A、B、C、D、Eの5人が1位から5位の順位を競った。以下の情報がある。
- BはCよりも速かった。
- AはDより遅かった。
- CはEよりも速かった。
- EはAよりも速かった。
このとき、正しい順位の可能性を選びなさい。
A. B > C > D > E > A
B. E > C > B > A > D
C. B > C > A > E > D
D. B > C > E > D > A
E. C > B > E > A > D
解答と解説を見る
解答: A, D
解説:
各選択肢が条件に適合するか確認します。
| 選択肢 | 順位関係 | B > C | A < D | C > E | E > A | 適合 |
| A | B > C > D > E > A | ○ | ○ | ○ | ○ | ✅ |
| B | E > C > B > A > D | × | × | ○ | ○ | ❌ |
| C | B > C > A > E > D | ○ | × | ○ | × | ❌ |
| D | B > C > E > D > A | ○ | ○ | ○ | ○ | ✅ |
| E | C > B > E > A > D | × | × | ○ | ○ | ❌ |
したがって、正解は A, D です。
SPIの推論【テストセンター】チェックボックス練習問題③
ある企業では、従業員の労働時間と休憩時間に関する以下のルールが決められている。
- 1日の労働時間は原則8時間までとする。
- 6時間以上働く場合、少なくとも45分の休憩を取る。
- 8時間を超えて労働する場合、時間外手当が支給される。
このとき、以下のうち正しいものをすべて選びなさい。
A. 1日9時間働いた場合、時間外手当が支給される。
B. 5時間勤務した場合、休憩は必須ではない。
C. 7時間働いた場合、30分の休憩を取ればよい。
D. 8時間勤務した場合、時間外手当は発生しない。
E. 6時間勤務した場合、休憩は45分未満でよい。
解答と解説を見る
解答: A, B, D
解説:
- Aは正しい → 8時間を超えた場合、時間外手当が発生するため。
- Bは正しい → 6時間未満の勤務では、休憩が義務付けられていないため。
- Cは誤り → 6時間以上働く場合、45分以上の休憩が必要なため、30分では不足する。
- Dは正しい → 8時間ちょうどの勤務では時間外手当は発生しない。
- Eは誤り → 6時間勤務の場合、必要な休憩時間は45分以上のため未満では不足する。
したがって、正解は A, B, D です。
SPIの推論【テストセンター】チェックボックス練習問題④
X、Y、Z、Wの4チームがリーグ戦を行った。結果について以下のことがわかっている。
- XはYに勝ち、Zに負けた。
- WはZに勝ち、Yに負けた。
- ZはYに勝った。
このとき、確実に言えることをすべて選びなさい。
A. ZはYより順位が高い。
B. WはXより順位が高い。
C. Yは全敗していない。
D. XはWに勝った。
E. WはZより順位が高い。
解答と解説を見る
解答: A, C
解説:
| チーム | X | Y | Z | W |
| X | – | ○ | × | ? |
| Y | × | – | × | 〇 |
| Z | ○ | ○ | – | × |
| W | ? | × | 〇 | – |
- Aは正しい → Zは2勝、Yは1勝のため順位が高い。
- Bは誤り → WがXと対戦した結果が不明なため、順位が確定しない。
- Cは正しい → YはWに勝っている。
- Dは誤り → XとWの試合結果が不明。
- Eは誤り → WがZより順位が高いとは限らない。
したがって、正解は A, C です。
SPIの推論【テストセンター】チェックボックス練習問題⑤
ある学校では、男子と女子の生徒の割合が以下の通りである。
| 性別 | 割合 |
| 男子 | 55% |
| 女子 | 45% |
この学校の生徒が800人いるとき、正しいものをすべて選びなさい。
A. 男子は440人である。
B. 女子は400人である。
C. 女子は360人である。
D. 男女の人数の差は80人である。
E. 男子は500人である。
解答と解説を見る
解答: A, C, D
解説:
- 男子 = 800 × 55% = 440人 → Aは正しい
- 女子 = 800 × 45% = 360人 → Cは正しい
- 男女の人数差 = 440 – 360 =80人 → Dは正しい
- B, Eは誤り
したがって、正解は A, C, D です。
- 今選考で出題されている問題が出る!「Lognavi」
「Lognavi」は今企業の選考で出題されているSPIの問題が出ると評判のアプリで、SPIの偏差値も出せるので、自分のレベルを知るためにも利用する価値があるアプリです。
Lognavi公式はこちら⇒https://lognavi.com/
- 最新のSPIを何度でも練習できる!「キャリアパーク」
「キャリアパーク」のSPIパーフェクト問題集は最新のSPIの問題が200問あり、解答や解説もついているので非常に学びになる無料の問題集です。
SPIの解答集つき問題集公式⇒https://careerpark.jp/
- 志望企業のSPIを通過できるかSPI判定もできる「キミスカ」
「キミスカ」はあなたが志望する企業のSPIのボーダーを突破できるか判定してくれる機能もあるサービスです。
キミスカ公式はこちら⇒https://kimisuka.com/
SPIの推論【テストセンター】チェックボックス練習問題⑥
ある会社では、5つの部署(A, B, C, D, E)にそれぞれ一定の人数が配置されている。各部署の人数は以下の条件を満たしている。
- A部署の人数はB部署の2倍である。
- C部署の人数はA部署より4人少ない。
- D部署の人数はB部署の3倍である。
- E部署の人数はC部署の半分である。
- 5つの部署の合計人数は66人である。
このとき、それぞれの部署の人数が正しいものをすべて選びなさい。
A. A部署の人数は14人である
B. B部署の人数は8人である
C. C部署の人数は12人である
D. D部署の人数は21人である
E. E部署の人数は6人である
F. 正しいものはない
解答と解説を見る
解答: B, C, E
解説:
- 設定:B部署の人数をxとする。
- A = 2x, C = A – 2, D = 3x, E = C / 2
- 合計人数の方程式:2x + x + (2x – 2) + 3x + (2x – 2)/2 = 66
- 解くと、B部署の人数は 8人 となる。
- A = 16人, C = 12人, D = 24人, E = 6人 となる。
したがって、正解は B, C, E。
SPIの推論【テストセンター】チェックボックス練習問題⑦
X、Y、Z、Wの4人が100点満点の英語試験を受けたところ、次のことが分かっている。
- 4人の平均点は72点だった。
- YとZの平均点は65点であった。
- WはXよりも12点高かった。
このとき、必ず正しいといえる推論の組み合わせをすべて選びなさい。
A. Xの得点は73点である
B. Yの得点は58点である
C. Zの得点は72点である
D. Wの得点は85点である
E. Wは全員の中で最高点である。
解答と解説を見る
解答: A,D
解説:
- 平均点 = (X + Y + Z + W) ÷ 4 = 72
- YとZの平均点 = (Y + Z) ÷ 2 = 65 → Y + Z = 130
- W = X + 12
これを用いて計算すると、
- X + Y + Z + W = 72 × 4 = 288
- X + (Y + Z) + W = 288
- X + 130 + (X + 12) = 288
- 2X + 142 = 288
- 2X = 146
- X = 73
- W = 73 + 12 = 85
YとZの得点は平均点しか分かっていないため特定することができない。
そのため、選択肢BとCは誤り。
また、YとZの得点が確定できないため、選択肢Eも誤り。
SPIの推論【テストセンター】チェックボックス練習問題⑧
A、B、C、D、Eの5人が横一列に並んでいる。以下の情報がある。
- AはBの左にいる。
- CはEの右にいる。
- DはAの右にいる。
- EはBの左にいる。
このとき、正しい並びの可能性をすべて選びなさい。
A. A – B – E – C – D
B. A – E – B – C – D
C. E – A – B – C – D
D. A – B – D – C – E
E. A – B – C – D – E
解答と解説を見る
解答: B,C
解説:
| 選択肢 | 並び順 | AはBの左 | CはEの右 | DはAの右 | EはBの左 | 適合 |
| A | A – B – E – C – D | ○ | ○ | ○ | × | ❌ |
| B | A – E – B – C – D | ○ | ○ | ○ | ○ | ✅ |
| C | E – A – B – C – D | ○ | ○ | ○ | ○ | ✅ |
| D | A – B – D – C – E | ○ | × | ○ | × | ❌ |
| E | A – B – C – D – E | ○ | × | ○ | × | ❌ |
したがって、正解は B, C。
SPIの推論【テストセンター】チェックボックス練習問題⑨
あるマラソン大会で、A、B、C、D、Eの5人が1位から5位の順位を競った。以下の情報がある。
- BはCよりも速かった。
- AはDより遅かった。
- EはAよりも速かった。
- CはEより遅かった。
このとき、正しい順位の可能性を選びなさい。
A. B > E > D > C > A
B. E > C > B > A > D
C. B > C > A > E > D
D. B > E > C > D > A
E. C > B > E > A > D
解答と解説を見る
解答: A, D
解説:
| 選択肢 | 順位関係 | B > C | A < D | E > A | C < E | 適合 |
| A | B > E > D > C > A | ○ | ○ | ○ | ○ | ✅ |
| B | E > C > B > A > D | × | × | ○ | ○ | ❌ |
| C | B > C > A > E > D | ○ | × | × | × | ❌ |
| D | B > E > C > D > A | ○ | ○ | ○ | ○ | ✅ |
| E | C > B > E > A > D | × | × | ○ | × | ❌ |
したがって、正解は A, D 。
SPIの推論【テストセンター】チェックボックス練習問題10
ある会社では、以下の勤務ルールが定められている。
- 1日の勤務時間は原則8時間である。
- 週に1日は必ず休みを取らなければならない。
- 残業は1日2時間までとする。
- 1か月の残業時間の合計は40時間を超えてはならない。
このとき、以下のうち正しいものをすべて選びなさい。
A. 1日10時間の残業をすることができる。
B. 1週間で7日間すべて勤務することはできない。
C. 1か月の残業時間が42時間になった場合、規則違反となる。
D. 1日の勤務時間は9時間でも規則に違反しない。
E. 1週間に2日以上休むことはできない。
解答と解説を見る
解答: B, C
解説:
A :1日10時間の残業はできない(最大2時間まで)→誤り
B : 週に1日は必ず休まなければならないので7日間勤務は不可 →正しい
C :1か月の残業時間が40時間を超えると規則違反 →正しい
D :1日の勤務時間は原則8時間のため、9時間勤務は規則違反 →誤り
E :週に2日以上休むことは可能(制限なし)→誤り
したがって、正解は B, C。
- 今選考で出題されている問題が出る!「Lognavi」
「Lognavi」は今企業の選考で出題されているSPIの問題が出ると評判のアプリで、SPIの偏差値も出せるので、自分のレベルを知るためにも利用する価値があるアプリです。
Lognavi公式はこちら⇒https://lognavi.com/
- 最新のSPIを何度でも練習できる!「キャリアパーク」
「キャリアパーク」のSPIパーフェクト問題集は最新のSPIの問題が200問あり、解答や解説もついているので非常に学びになる無料の問題集です。
SPIの解答集つき問題集公式⇒https://careerpark.jp/
- 志望企業のSPIを通過できるかSPI判定もできる「キミスカ」
「キミスカ」はあなたが志望する企業のSPIのボーダーを突破できるか判定してくれる機能もあるサービスです。
キミスカ公式はこちら⇒https://kimisuka.com/
SPIの推論【テストセンター】チェックボックス練習問題11
あるレースで、A、B、C、D、Eの5人が1位から5位の順位を競った。以下の情報がある。
- BはCよりも速かった。
- AはDより遅かった。
- EはAよりも速かった。
- CはEより遅かった。
このとき、正しい順位の可能性を選びなさい。
A. B > E > D > C > A
B. E > C > B > A > D
C. B > C > A > E > D
D. B > E > C > D > A
E. C > B > E > A > D
解答と解説を見る
解答: A, D
解説:
| 選択肢 | 順位関係 | B > C | A < D | E > A | C < E | 適合 |
| A | B > E > D > C > A | ○ | 〇 | ○ | 〇 | ✅ |
| B | E > C > B > A > D | × | × | ○ | ○ | ❌ |
| C | B > C > A > E > D | ○ | × | × | × | ❌ |
| D | B > E > C > D > A | ○ | ○ | ○ | 〇 | ✅ |
| E | C > B > E > A > D | × | × | ○ | × | ❌ |
したがって、正解は A, D 。
SPIの推論【テストセンター】チェックボックス練習問題12
あるスポーツ大会で、A、B、C、D、Eの5チームが総当たり戦を行った。以下の結果が分かっている。
- AはBに勝ったが、C、D、Eには負けた。
- BはDに勝ったが、CとEに負けた。
- CはAとDに勝ったが、Eに負けた。
- DはAとEに勝ったが、Bに負けた。
- EはAとCに勝ったが、Dに負けた。
このとき、勝利数が最も多かったチームをすべて選びなさい。
A. A
B. B
C. C
D. D
E. E
解答と解説を見る
解答: C, E
解説:
| チーム | A | B | C | D | E | 勝利数 |
| A | – | ○ | × | × | × | 1勝 |
| B | × | – | × | ○ | × | 1勝 |
| C | ○ | ○ | – | ○ | × | 3勝 |
| D | ○ | × | × | – | ○ | 2勝 |
| E | ○ | ○ | ○ | × | – | 3勝 |
CとEが最も多くの勝利を収めたため、正解は C, E。
SPIの推論【テストセンター】チェックボックス練習問題13
ある企業では、社員の年齢層ごとの割合が以下のように分かれている。
| 年齢層 | 割合 |
| 20代 | 35% |
| 30代 | 25% |
| 40代 | 30% |
| 50代 | 10% |
この企業の社員数が600人であるとき、以下の推論のうち正しいものをすべて選びなさい。
A. 30代の社員は150人である。
B. 20代と40代の社員を合わせると330人になる。
C. 50代の社員数は60人である。
D. 20代と30代の社員を合わせると360人になる。
E. 40代の社員は160人である。
解答と解説を見る
解答: A, C, D
解説:
- 各年齢層の社員数を計算する。
- 20代: 600 × 35% = 210人
- 30代: 600 × 25% = 150人
- 40代: 600 × 30% = 180人
- 50代: 600 × 10% = 60人
- 選択肢ごとの判定
- A: 30代の社員は 150人 → 正しい。
- B: 20代(210人) + 40代(180人) = 390人 → 誤り。
- C: 50代の社員は 60人 → 正しい。
- D: 20代(210人) + 30代(150人) = 360人 → 正しい。
- E: 40代の社員は 180人 なので、160人ではない → 誤り。
したがって、正解は A, C, D 。
SPIの推論【テストセンター】チェックボックス練習問題14
ある工場で、A、B、C、D、Eの5つのラインで商品を生産している。以下の条件が分かっている。
- Aラインの生産数はBラインの2倍である。
- Cラインの生産数はAラインより6個少ない。
- Dラインの生産数はBラインの3倍である。
- Eラインの生産数はCラインの半分である。
- 5つのラインの合計生産数は99個である。
このとき、それぞれのラインの生産数が正しいものをすべて選びなさい。
A. Aラインの生産数は20個である。
B. Bラインの生産数は12個である。
C. Cラインの生産数は15個である。
D. Dラインの生産数は30個である。
E. Eラインの生産数は9個である。
解答と解説を見る
解答: B, E
解説:
- Bの生産数をxとする。
- A = 2x, C = A – 6, D = 3x, E = C / 2
- 合計生産数の方程式:2x + x + (2x – 6) + 3x + (2x – 6)/2 = 99
- 解くと、Bの生産数は 12個 となる。
- A = 24個, C = 18個, D = 36個, E = 9個 となる。
したがって、正解は B, E 。
SPIの推論【テストセンター】チェックボックス練習問題15
ある会社で、5人の社員の1週間の勤務時間が以下の通りであった。
38時間, 44時間, 36時間, 42時間, 40時間
このとき、以下のうち正しいものをすべて選びなさい。
A. 平均勤務時間は40時間である。
B. 平均勤務時間は38時間である。
C. 最長勤務時間は44時間である。
D. 最短勤務時間は38時間である。
E. 中央値は36時間である。
解答と解説を見る
解答: A, C
解説:
- 平均を求める
- (38 + 44 + 36 + 42 + 40) ÷ 5 = 200 ÷ 5 = 40時間 → Aは正しい、Bは誤り。
- 最長勤務時間
- 最も長い勤務時間は 44時間 → Cは正しい。
- 最短勤務時間
- 最も短い勤務時間は 36時間 なので、Dの38時間は誤り。
- 中央値を求める
- 昇順に並べると 36, 38, 40, 42, 44
- 中央の値は 40時間 → Eは誤り。
したがって、正解は A, C 。
SPIの推論【テストセンター】チェックボックス練習問題16
A、B、C、D、Eの5人が1列に並んでいる。以下の条件が分かっている。
- AはBの左にいる。
- CはDの右にいる。
- DはEの左にいる。
- BはCの左にいる。
このとき、可能な並び順をすべて選びなさい。
A. A – B – C – D – E
B. A – D – B – C – E
C. B – A – C – D – E
D. A – B – D – C – E
E. A – B – C – E – D
解答と解説を見る
解答: B, D
解説:
以下の条件を満たしているかを確認する。
| 選択肢 | AはBの左 | CはDの右 | DはEの左 | BはCの左 | 適合 |
| A – B – C – D – E | ○ | × | ○ | ○ | × |
| A – D – B – C – E | ○ | ○ | ○ | ○ | ○ |
| B – A – C – D – E | × | × | ○ | ○ | × |
| A – B – D – C – E | ○ | ○ | ○ | ○ | ○ |
| A – B – C – E – D | ○ | × | × | ○ | × |
したがって、正解は B, D 。
SPIの推論【テストセンター】チェックボックス練習問題17
あるマラソン大会で、A、B、C、D、Eの5人がゴールした。以下のことが分かっている。
- AはCより先にゴールした。
- BはDより後にゴールした。
- Aは最も早くゴールした。
- CはDよりも先にゴールした。
このとき、可能な順位をすべて選びなさい。
A. A – C – D – B – E
B. A – D – C – B – E
C. C – A – D – B – E
D. A – B – C – D – E
E. A – C – E – D – B
解答と解説を見る
解答: A, E
解説:
以下の条件を満たしているかを確認する。
| 選択肢 | AはCより先 | BはDより後 | Aが最も早い | CはDより先 | 適合 |
| A – C – D – B – E | ○ | ○ | ○ | ○ | ○ |
| A – D – C – B – E | ○ | ○ | ○ | × | ○ |
| C – A – D – B – E | × | ○ | × | ○ | × |
| A – B – C – D – E | ○ | × | ○ | ○ | × |
| A – C – E – D – B | ○ | ○ | ○ | ○ | ○ |
したがって、正解は A, E 。
SPIの推論【テストセンター】チェックボックス練習問題18
ある企業の販売成績に関する報告書を以下のように要約した。
- X、Y、Zの3つの営業部門がある。
- X部門の売上はY部門より高い。
- Z部門の売上はX部門より低い。
- Y部門の売上はZ部門の売上より高い。
このとき、以下のうち正しいものをすべて選びなさい。
A. X部門の売上が最も高い。
B. Z部門の売上が最も低い。
C. Y部門の売上はX部門より高い。
D. Y部門の売上はZ部門より高い。
E. Z部門の売上はY部門より高い。
解答と解説を見る
解答: A, B, D
解説:
- 問題文からX > Y > Zの関係が成り立つ。
- A: Xが最も高いので 正しい。
- B: Zが最も低いので 正しい。
- C: YはXより低いので 誤り。
- D: YがZより高いので 正しい。
- E: ZはYより低いので 誤り。
したがって、正解は A, B, D 。
SPIの推論【テストセンター】チェックボックス練習問題19
あるサッカーリーグで、赤、青、黄、緑、白の5チームが対戦した。以下の結果が分かっている。
- 赤は青に勝ったが、緑と白に負けた。
- 青は緑に勝ったが、赤と黄に負けた。
- 黄は赤と緑に勝ったが、白に負けた。
- 緑は赤と白に勝ったが、黄に負けた。
- 白は赤と青に勝ったが、緑に負けた。
このとき、最も多くの試合に勝ったチームをすべて選びなさい。
A. 赤
B. 青
C. 黄
D. 緑
E. 白
解答と解説を見る
解答: C.黄, E.白
解説:
| チーム | 赤 | 青 | 黄 | 緑 | 白 | 勝利数 |
| 赤 | – | ○ | × | × | × | 1勝 |
| 青 | × | – | × | ○ | × | 1勝 |
| 黄 | ○ | ○ | – | ○ | × | 3勝 |
| 緑 | ○ | × | × | – | ○ | 2勝 |
| 白 | ○ | ○ | ○ | × | – | 3勝 |
黄と白が最も多くの勝利を収めたため、正解は C, E 。
SPIの推論【テストセンター】チェックボックス練習問題20
ある会社では、社員の年齢層ごとの割合が以下のように分かれている。
| 年齢層 | 割合 |
| 20代 | 30% |
| 30代 | 25% |
| 40代 | 35% |
| 50代 | 10% |
この企業の社員数が800人であるとき、以下の推論のうち正しいものをすべて選びなさい。
A. 30代の社員は200人である。
B. 20代と40代の社員を合わせると440人になる。
C. 50代の社員数は80人である。
D. 20代と30代の社員を合わせると480人になる。
E. 40代の社員は280人である。
解答と解説を見る
解答: A, C, E
解説:
- 各年齢層の社員数を計算する。
- 20代: 800 × 30% = 240人
- 30代: 800 × 25% = 200人
- 40代: 800 × 35% = 280人
- 50代: 800 × 10% = 80人
- 選択肢ごとの判定
- A: 30代の社員は 200人 → 正しい。
- B: 20代(240人) + 40代(280人) = 520人 → 選択肢の人数と違うので 誤り。
- C: 50代の社員は 80人 → 正しい。
- D: 20代(240人) + 30代(200人) = 440人 → 選択肢の人数と違うので 誤り。
- E: 40代の社員は 280人 → 正しい。
したがって、正解は A, C, E 。
SPIの推論の練習を繰り返すメリット
SPIの非言語分野における推論問題は、単純な計算問題とは異なり、複数の条件を同時に整理し、矛盾しない解を導く力が求められる問題です。
推論問題を繰り返し練習することで、この構造化のプロセスが徐々にスムーズになり、複雑な条件が提示された場合でも冷静に分析し、筋道を立てて考える能力が磨かれていきます。
これは単なる試験対策にとどまらず、日常生活やビジネスシーンでも活かせる普遍的な思考力を身につけることにつながるのです。
推論問題を解こうとすると、頭の中に一時的な作業領域が必要となり、そこに条件や数字を置きながら、辻褄が合うかどうかを確認していきます。
この過程で自然と抽象的な思考の訓練が行われ、論理的に筋道を組み立てる習慣が身につきます。練習を重ねることで、複雑に見える情報でも整理して意味のある形に構造化できるようになり、「問題を解くための思考の流れ」が体の中に定着していきます。
このように推論問題の反復練習は、思考力そのものの強化に直結する大きなメリットがあります。
パターン認識が身につき問題処理のスピードが向上します
推論問題は種類ごとに特徴があり、条件付きの組み合わせ問題、順序決定問題、位置関係の整理問題など、一定の型が存在します。
このパターン認識が身につくと、「あ、このタイプなら表を作って整理した方が早い」「この問題は確定情報から順に埋めていけば解ける」といった判断が素早くできるようになります。
最初のうちは一問を解くのに時間がかかっていたとしても、練習を重ねることで処理の速度が大幅に向上し、時間制限のあるSPI本番でも落ち着いて対応できるようになります。
SPIは制限時間が厳しく、特に非言語分野では時間が足りなくなりやすいため、スピードの向上は大きな武器になります。
推論問題は丁寧に取り組もうとすると時間がかかりますが、練習を通じて「考え方の型」を身につけることで、自然と処理が自動化に近い形で進むようになります。これは試験本番の得点力アップに直結する大きなメリットです。
情報の取捨選択が上手になり問題解決力が高まります
推論問題の特徴のひとつに、問題文に多くの情報が散りばめられていることがあります。しかし、その中のすべてが答えに必要なわけではなく、むしろ意図的に不要な情報が含まれている場合もあります。
この「情報整理力」は、試験に限らずビジネスでも非常に重要な能力です。現代の職場では、多くのデータや報告が飛び交う中で、必要な情報だけを見抜き、判断につながる材料へと整理するスキルが求められます。
推論問題を通じて情報の本質を見抜く力が育つことで、将来的にも役立つ知的基盤が形成されます。練習は単に問題を解く力を身につける行為ではなく、自分の思考習慣そのものをアップデートしていく行為なのです。
時間制限下での集中力と精神的耐性が鍛えられます
SPIは短時間で多くの問題を処理する必要があるため、精神的なプレッシャーが大きい試験です。
しかし、日常的に推論問題を解く練習を続けていると、時間制限のある状況に対して慣れが生まれ、プレッシャーに強くなります。
また、推論問題を解く過程では「詰まってしまう」「間違ってしまう」といった体験を何度も味わいますが、この経験を繰り返すことで、ミスや停滞に対する耐性がついていきます。
間違えたときに冷静に戻り、なぜ間違えたのかを分析する習慣が身につくと、試験本番でも焦らず対処できるようになります。
この精神的な耐性は、試験後のキャリアでも役に立つ力であり、自分の思考過程を客観的に見つめる力にもつながります。
思考の基盤が強固になり将来の学習や仕事でも役立ちます
推論問題を練習するメリットは、試験のためだけではありません。問題の多くは「条件の整理」「矛盾の排除」「論理的な結論」という思考プロセスで構成されているため、これらに慣れていくと、様々な場面で問題解決力が向上します。
練習によって「わからないものを理解するための手順」が明確になり、自分の思考を整理する力が自然と高まっていきます。
これは非常に大きな財産であり、長期的なキャリアにおいても強みとなります。SPIの対策をする時間は短期的には大変かもしれませんが、得られる思考力は長い目で見て自分を支える基盤となるものです。
試験本番での安定したパフォーマンスにつながります
推論問題は非言語分野の中でも特に時間を要する問題領域であるため、ここが苦手だと全体の時間配分に大きな悪影響が出ます。しかし、練習を通じて推論問題への耐性と処理スピードが身につくと、試験当日にも余裕が生まれます。
余裕があることでミスが減り、落ち着いて全体を見渡しながら解くことができるようになります。
また、難しい問題を自力で解けるようになる過程では、成長実感が得られやすく、自信が生まれます。
この自信は本番で非常に重要な力となり、「自分は解ける」という前向きな意識が集中力を高め、安定したパフォーマンスにつながります。練習によって作り上げた思考の型や経験は、試験中の一問一問を支えてくれる頼もしい味方になります。
推論問題練習の価値
SPI非言語の推論問題を繰り返し練習することは、単なる試験対策ではなく、論理的思考力、情報処理能力、パターン認識力、精神的耐性、時間管理力といった多面的な能力を育てる知的訓練となります。
こうした力はSPI本番だけでなく、社会人として仕事を進める上でも大いに役立つものです。推論問題の練習は時間と労力を必要としますが、その分だけ得られるものも大きく、自分の思考の基盤を強くする投資と言えます。
繰り返し取り組むことで、確かな成長と自信を手にすることができるため、継続して練習することに大きな意味があります。
- 今選考で出題されている問題が出る!「Lognavi」
「Lognavi」は今企業の選考で出題されているSPIの問題が出ると評判のアプリで、SPIの偏差値も出せるので、自分のレベルを知るためにも利用する価値があるアプリです。
Lognavi公式はこちら⇒https://lognavi.com/
- 最新のSPIを何度でも練習できる!「キャリアパーク」
「キャリアパーク」のSPIパーフェクト問題集は最新のSPIの問題が200問あり、解答や解説もついているので非常に学びになる無料の問題集です。
SPIの解答集つき問題集公式⇒https://careerpark.jp/
- 志望企業のSPIを通過できるかSPI判定もできる「キミスカ」
「キミスカ」はあなたが志望する企業のSPIのボーダーを突破できるか判定してくれる機能もあるサービスです。
キミスカ公式はこちら⇒https://kimisuka.com/
【SPI推論のコツ】難しい例題・練習問題で解き方を解説まとめ
SPIの推論のコツや解き方、練習問題などは参考になりましたでしょうか。
SPIの推論は苦手な人は本当に苦手だと思います。しかしここで諦めてしまっては就職したい就職先の選考で落とされてしまう可能性が高いです。
各社SPIのボーダーを設けているため、このボーダーを突破しない限り落とされてしまうので、今回ご紹介している練習問題などを活用してぜひ推論を克服できるようにしましょう。
また、スマホでこのページを見てくださっている方限定で今まさに出題されているSPIの練習ができると評判のアプリを紹介します。
このアプリはSPIの練習だけでなく、10段階評価で自分のSPIの偏差値も出してくれて、志望企業のボーダーを突破できるのかも分かる便利アプリです。
この問題と「無料で手に入るSPIの問題集」だけやっておけばWEBテストは安心なので、スマホでこのページを見たこの機会に是非「SPIの練習ができると評判のアプリ」と「無料で手に入るSPIの問題集」を試してみてくださいね。

下記のURLからアプリインストール画面に飛べるので、今のうちにインストールして初回起動だけでもしておきましょう!
自分のSPIの出来を今のうちに判断した方が正確で対策しやすいですよ。
URLはこちら⇒https://lognavi.com/
\ 先ずはインストール /
SPI対策に時間をかけたくない場合は2月の今のうちに無料で手に入るSPIの解答集つき問題集をやっておくと就活が楽になりますよ。
▼25卒に大人気でした▼
今まさに出題されているSPIの問題があるのでチェックしておいてください。
上記の問題集は解答もあるので、正直解答集みたいなもので、あまり大声では言えませんが、26卒・27卒はこの解答を憶えれば勝てちゃいますね。
SPI問題集公式⇒https://careerpark.jp/
\ 26卒・27卒に推奨 /
SPI試験を開発したリクルートマネジメントソリューションズの企業情報
| 会社名 | 株式会社リクルートマネジメントソリューションズ |
| 英文社名 | Recruit Management Solutions Co., Ltd. |
| 創業 | 1963年 |
| 設立 | 1989年 |
| 資本金 | 1億5千万円 |
| 売上高 | 212億1千万円(2023年3月期) |
| 従業員数 | 585名(2023年4月1日時点) |
| 代表者 | 代表取締役社長 山﨑 淳 |
| 本社所在地 | 〒108-0023 東京都港区芝浦3-16-16 住友不動産田町ビル東館 4F (登記上本社)東京都千代田区丸の内1-9-2 0120-878-300 TEL:03-6331-6000 |
| 拠点所在地 | 東海 〒460-0008 愛知県名古屋市中区栄2-1-1 日土地名古屋ビル 関西 〒530-8240 大阪府大阪市北区角田町8-1 大阪梅田ツインタワーズ・ノース 新潟・山形(庄内)<オフィシャルパートナー> 株式会社マネジメントソリューションズ 〒951-8122 新潟県新潟市中央区旭町通1番町754-27 メゾン・ド・コリン201 |
| 研究所 | ■組織行動研究所 組織・人材マネジメント領域において幅広く調査・研究・情報発信を行う弊社の研究部門です。1963年のアセスメント事業の発足以来、組織行動学、産業組織心理学などの情報収集を行ってきた研究・開発部門を母体に、2004年に設立しました。 ■測定技術研究所 心理測定技術をベースとしたアセスメントやサーベイの商品開発および品質の維持・向上,測定技法や経営人事テーマに関する調査・研究を行う弊社の研究部門です。1964年に日本リクルートセンターに発足したテスト部の開発部門を前身とし、総合検査SPIなどを開発してきました。 ■HR Analytics & Technology Lab 人事課題の解決をアナリティクスによって加速させるため、アセスメントやサーベイを中心とした人事データ利活用の推進を行う技術開発部門です。2017年に発足し、開発した分析技術の学会発表やクライアント提供を主に行っています。 |
| Webサイト | https://www.recruit-ms.co.jp/ |


















コメント