この記事では27卒や28卒のために適性検査・WEBテストのSPI非言語の練習問題を解説つきで無料で公開します。
SPI非言語の推論など頻出分野の練習問題・例題や過去問を網羅して公開するので形式になれるために模擬試験として練習していただければと思います。
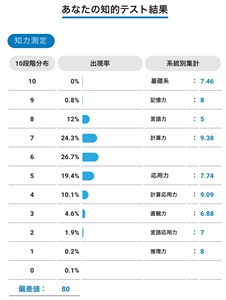
SPIの非言語の頻出問題集はこちらのアプリから行う事ができます。SPIの摸試が行えて10段階評価で行きたい企業のボーダーを超えてるか正確に自分の偏差値がわかるからおすすめです。こちらからインストールして活用してくださいね。
また、スマホでこのページを見てくださっている方限定で今まさに出題されているSPIの練習ができると評判のアプリを紹介します。
このアプリはSPIの練習だけでなく、10段階評価で自分のSPIの偏差値も出してくれて、志望企業のボーダーを突破できるのかも分かる便利アプリです。
この問題と「無料で手に入るSPIの問題集」だけやっておけばWEBテストは安心なので、スマホでこのページを見たこの機会に是非「SPIの練習ができると評判のアプリ」と「無料で手に入るSPIの問題集」を試してみてくださいね。

下記のURLからアプリインストール画面に飛べるので、今のうちにインストールして初回起動だけでもしておきましょう!
自分のSPIの出来を今のうちに判断した方が正確で対策しやすいですよ。
URLはこちら⇒https://lognavi.com/
\ 先ずはインストール /
SPI対策に時間をかけたくない場合は2月の今のうちに無料で手に入るSPIの解答集つき問題集をやっておくと就活が楽になりますよ。
▼25卒に大人気でした▼
今まさに出題されているSPIの問題があるのでチェックしておいてください。
上記の問題集は解答もあるので、正直解答集みたいなもので、あまり大声では言えませんが、26卒・27卒はこの解答を憶えれば勝てちゃいますね。
SPI問題集公式⇒https://careerpark.jp/
\ 26卒・27卒に推奨 /
【関連記事】
- 【SPI推論のコツ】難しい例題・練習問題で解き方を解説
- SPIテストセンターで2タブばっかり!非言語の推論で2タブはやばいのか解説
- SPIテストセンターで推論ばかり出る理由!チェックボックスが出れば7割以上期待できる?
SPI非言語は練習問題を繰り返さないと危険?失敗しないための前知識
SPI非言語は、就職活動におけるWEB適性検査の中でも、特に対策の有無によって結果に大きな差が出やすい分野です。
しかし、そのような考え方こそが、SPI非言語において失敗しやすい最大の要因であると言えます。
この特徴を理解せずに臨んでしまうと、「解き方は分かるのに時間が足りない」「焦って計算ミスをしてしまう」といった事態が起こりやすくなります。その結果、本来の実力よりも低い評価を受けてしまう危険性が高まります。
SPI非言語は「知っている」だけでは通用しない試験
SPI非言語が難しいと感じられる理由の一つに、「解き方を知っていること」と「本番で解けること」がまったく別である点が挙げられます。
割合や損益、仕事算、推論といった問題は、学校で一度は学んだことのある内容がほとんどです。しかし、SPIではそれらが独特の文章構成や制限時間の中で出題されます。
特に初見の場合、問題文を読んで状況を整理するまでに時間がかかり、その時点で焦りが生まれてしまいます。
焦りは判断ミスや計算ミスにつながりやすく、結果として得点が伸びません。SPI非言語では、「知識があるかどうか」よりも、「条件反射的に解法を選べるかどうか」が重要になるため、練習問題を繰り返して体に覚えさせることが不可欠なのです。
練習不足が招く典型的な失敗パターン
SPI非言語を十分に練習せずに受検した場合、いくつかの典型的な失敗パターンに陥りやすくなります。
SPI非言語は問題数に対して制限時間が短いため、時間配分を誤ると、それだけで大きな失点につながります。
また、問題形式に慣れていないことで、「この問題はどの解法を使うべきか」という判断に迷ってしまうこともあります。
練習を積んでいれば、問題文を読んだ瞬間に「これは割合の問題です」「これは推論です」と見分けられるようになりますが、経験が不足していると、考え始めるまでに余計な時間がかかってしまいます。
こうした積み重ねが、結果的に不利な評価を招くのです。
SPI非言語で本当に見られているポイント
SPI非言語で企業が見ているのは、計算が速いかどうかだけではありません。与えられた情報を整理し、必要な要素だけを抜き出し、論理的に答えを導く力があるかどうかが重視されています。
これは、実際の業務においても非常に重要な能力です。
そのため、SPI非言語では「難しい問題を解けるか」よりも、「基本的な問題を安定して、速く、正確に処理できるか」が評価のポイントになります。
この安定感は、一度や二度問題を解いただけでは身につきません。繰り返し練習を行い、どの形式でも落ち着いて対応できる状態を作ることが重要です。
なぜSPI非言語は繰り返し練習が必要なのか
SPI非言語で安定した得点を取るためには、練習問題を繰り返すことがほぼ必須と言えます。
問題自体の難易度は決して極端に高くありませんが、制限時間、問題文の長さ、選択肢の構成など、独特のクセがあります。
繰り返し練習をすることで、問題文の読み方、計算の進め方、時間配分の感覚が徐々に身についていきます。
すると、本番では一問ごとに考え込むことが減り、自然とテンポよく解き進められるようになります。
この状態になって初めて、SPI非言語を「危険な試験」ではなく、「対策すれば得点源になる分野」として捉えられるようになります。
本番で失敗しないために持っておくべき前知識
SPI非言語で失敗しないためには、「完璧を目指さなくてよい」という前知識も重要です。
練習を通して、自分が得点しやすい問題と時間がかかりやすい問題を把握しておくことで、本番での判断がしやすくなります。
また、計算力だけでなく、問題文を正確に読む力が重要であることも理解しておく必要があります。
SPI非言語では、条件の読み落としや勘違いによるミスが非常に起こりやすいため、落ち着いて処理する姿勢が求められます。この落ち着きも、繰り返し練習をして「見慣れた状況」を作ることで身につくものです。
SPI非言語は「準備した人ほど有利になる分野」
SPI非言語は、才能やセンスだけで差がつく分野ではありません。むしろ、どれだけ事前に練習を積み、問題形式に慣れているかが結果に直結します。
練習問題を繰り返さずに臨むことは、自分の実力を正しく評価してもらう機会を自ら減らしてしまう行為とも言えます。
このように、SPI非言語は練習問題を繰り返さないと危険になりやすい分野である一方、正しい前知識を持ち、計画的に対策を行えば、安定して得点を伸ばしやすい分野でもあります。
本番で後悔しないためにも、SPI非言語の特徴を理解し、繰り返し練習を重ねて万全の状態で臨むことが大切です。
スマホでこのページを見ている方限定でお伝えしたいのが、今まさに出題されているSPIの問題が出ると評判の「Lognavi」というアプリです。
MBTI顔負けの性格診断も出来て、あなたの市場価値まで企業側に伝わって超大手優良企業からのオファーももらえちゃうから一石二鳥です!

下記のURLからアプリインストール画面に飛べるので、今のうちにインストールして初回起動だけでもしておきましょう!
自分のSPIの出来を今のうちに判断した方が正確で対策しやすいですよ。
アプリインストールはこちらから⇒https://lognavi.com/
※インストール後の初回起動はお早めに
\ 先ずはインストール /
ESや企業研究でSPIに時間を割く暇がないと思うので、今選考で出題されているSPIの練習が無料でできるSPIの無料問題集をやっておいてください。
無料でダウンロードできるので、SPIに時間をかけたくない場合は使ってみてください。
▼25卒に大人気でした▼
参考書や問題集と違って問題が最新版にアップデートされるので、今どのような問題が出題されているのか、頻出問題ばかりなのでチェックするためにも利用すると良いでしょう。
とくにWEBテストは出題される問題の難易度もまばらなので、長文や推論などが苦手な学生ほど使っておく事をおすすめします。
一応リンク貼っておくので、自由に使ってみてください。
SPI問題集公式⇒https://careerpark.jp/
こちらの記事も参考にしてくださいね。
SPI非言語の推論など頻出分野の練習問題・解説一覧
SPI非言語には、毎年のように繰り返し出題される「頻出形式」が存在します。これらを事前に知っておくことで、対策の効率が大きく上がり、本番でも落ち着いて対応しやすくなります。
・割合・比に関する問題
売上の増減、値引き、構成比などを題材にした問題が多く出題されます。どの数値を基準にして割合を考えるのかを正しく理解できていないと間違えやすいため、文章を丁寧に読み取る力が重要になります。
・損益算の問題
原価、定価、利益率などを使って利益や売値を求める形式です。考え方は割合問題と共通している部分が多く、基本パターンを理解していれば比較的安定して解けるようになります。
・仕事算の問題
複数人や複数日で作業を行った場合の所要時間を求める問題です。条件を整理して考える力が必要で、慣れていないと時間がかかりやすいですが、頻出形式のため対策効果が高い分野です。
・速さに関する問題
移動時間や到達時間、速さの違いを扱う問題が出題されます。公式自体はシンプルですが、状況を正しくイメージしないと混乱しやすいため、問題文の読み取りが重要です。
・推論問題
複数の条件から正しい結論を導く形式で、論理的思考力が問われます。テストセンター方式では、正答率が高い場合により複雑な推論問題が出題されることもあります。
このように、SPI非言語では基礎的な数学内容をもとにした頻出形式が数多く存在します。どれも難解な知識を必要とするものではありませんが、制限時間内に安定して解けるかどうかが重要です。頻出形式を理解し、練習を重ねて慣れておくことで、SPI非言語を得点源に変えていくことができるでしょう。
SPI非言語の練習問題【頻出分野】「割合と比」
練習問題①
ある企業の営業成績を調べたところ、3か月間の売上の合計は2960万円で、2か月目は1か月目の1.5倍、3か月目は2か月目の0.8倍だった。このとき、1か月目の売上は何万円か。
【選択肢】
A. 600 B. 700 C. 800 D. 900 E. 1000
解答と解説を見る
【解答】C. 800
【解説】
1か月目をxとすると、2か月目は1.5x、3か月目は1.2x(=1.5x×0.8)
合計売上は x + 1.5x + 1.2x = 3.7x
3.7x = 2960 より、x = 2960 ÷ 3.7 = 800
したがって、1か月目の売上は800万円
練習問題②
あるイベントの参加者は男性と女性の比が3:2で、参加者の40%が学生だった。学生のうち男性が60人いたとすると、参加者の総数は何人か。
【選択肢】
A. 250 B. 300 C. 350 D. 400 E. 450
解答と解説を見る
【解答】A. 250
【解説】
参加者の総数をx人とする。
そのうち40%が学生なので、学生数は0.4x人
学生のうち、男性:女性=3:2なので、男性学生は0.4x×(3/5)=0.24x
これが60人なので、0.24x = 60 → x = 60 ÷ 0.24 = 250
したがって、参加者の総数は250人
練習問題③
ある会社で製品Aと製品Bを製造している。AとBの製造数の比は5:3で、A1個あたりの利益は800円、B1個あたりの利益は1200円である。このとき、全体の利益に占めるAの利益の割合は何%か。(答えは小数点第1位を四捨五入すること)
【選択肢】
A. 50.0% B. 53.0% C. 55.0% D. 57.0% E. 60.0%
解答と解説を見る
【解答】B. 53.0%
【解説】
AとBの個数をそれぞれ5x、3xとすると、Aの利益=5x×800=4000x、Bの利益=3x×1200=3600x。
合計利益=4000x + 3600x = 7600x。
Aの利益割合=4000x ÷ 7600x ×100=52.63… → 小数点第1位を四捨五入して53.0%
練習問題④
ある展示会では、初日の来場者数が全体の40%、2日目は初日の0.75倍、3日目は残りの人数だった。このとき、3日目の来場者数は全体の何%か。
【選択肢】
A. 20.0% B. 25.0% C. 30.0% D. 35.0% E. 40.0%
解答と解説を見る
【解答】C. 30.0%
【解説】
全体を100人と仮定
初日=40人、2日目=40×0.75=30人 → 合計70人
残り=100−70=30人 → 3日目は全体の30%
練習問題⑤
A町とB町の人口は2:3の比である。A町の人口のうち15%が高齢者で、B町の人口のうち10%が高齢者だった。2つの町を合わせたとき、高齢者の割合はおおよそ何%か。
【選択肢】
A. 11.0% B. 12.0% C. 13.0% D. 14.0% E. 15.0%
解答と解説を見る
【解答】B. 12.0%
【解説】
人口をA=200人、B=300人と仮定
Aの高齢者=200×0.15=30人、Bの高齢者=300×0.10=30人
合計人口=500人、合計高齢者=60人 → 60/500×100=12%
練習問題⑥
ある会社の男性社員と女性社員の比は7:3で、男性は210人いる。女性の人数は?
A. 80
B. 85
C. 90
D. 95
E. 100
解答と解説を見る
【解答】C
【解説】男性:女性=7:3。男性210→1単位=30。女性=3×30=90。
練習問題⑦
2種類の食塩水を混ぜる。濃度8%の食塩水200gと、濃度12%の食塩水300gを混ぜたときの濃度で最も近いものは?
A. 9%
B. 9.5%
C. 10%
D. 10.5%
E. 11%
解答と解説を見る
【解答】D
【解説】食塩量=200×0.08+300×0.12=16+36=52。全体=500。濃度=52/500=0.104=10.4% ≈10.5%。
練習問題⑧
ある町の人口は、昨年から20%増加して6万人になった。昨年の人口は?
A. 48,000
B. 49,000
C. 50,000
D. 51,000
E. 52,000
解答と解説を見る
【解答】C
【解説】昨年をxとすると1.2x=60,000。x=50,000。
練習問題⑨
ある商品を定価の80%で売ったところ、原価の20%の利益が得られた。この商品の原価は?(定価は2,400円)
A. 1,600
B. 1,700
C. 1,800
D. 1,900
E. 2,000
解答と解説を見る
【解答】A
【解説】販売価格=2,400×0.8=1,920。原価をxとすると1,920=1.2x。x=1,600。
練習問題10
AとBの人数比は3:2で、Cの人数はAとBの合計の半分である。3人合計が90人のとき、Cの人数は?
A. 20
B. 25
C. 28
D. 30
E. 32
解答と解説を見る
【解答】D
【解説】A:B=3:2→合計5k。C=(A+B)/2=2.5k。合計=7.5k=90→k=12。C=2.5×12=30。
SPI非言語の練習問題【頻出分野】「損益算」
練習問題①
ある商品を定価の15%引きで販売したところ、原価の30%の利益が出た。この商品の定価が1300円のとき、原価はいくらか。
【選択肢】
A. 800円 B. 850円 C. 900円 D. 950円 E. 1000円
解答と解説を見る
【解答】B. 850円
【解説】
売値=1300×0.85=1105円
原価=aとすると、利益=1105−a=0.3a
よって、1105=1.3a → a=1105÷1.3=850円
練習問題②
原価600円の商品を、定価の20%引きで販売したところ、40円の損失が出た。このときの定価はいくらか。
【選択肢】
A. 680円 B. 700円 C. 720円 D. 740円 E. 760円
解答と解説を見る
【解答】B. 700円
【解説】
売値=原価−損失=600−40=560円
定価の20%引きで560円なので、定価×0.8=560
定価=560÷0.8=700円
よって、答えは700円
練習問題③
原価850円の商品を、定価の15%引きで販売して20%の利益を得るためには、定価をいくらにすればよいか。
【選択肢】
A. 1050円 B. 1100円 C. 1150円 D. 1200円 E. 1250円
解答と解説を見る
【解答】D. 1200円
【解説】
定価=x円とする。売値=0.85x
この売値で原価850円に対し20%の利益を得るには、
0.85x = 850 × 1.2 = 1020 → x = 1020 ÷ 0.85 = 1200円
よって定価は1200円
練習問題④
ある商品を1200円で仕入れ、50%の利益が出るように定価をつけた。その後、在庫処分のため定価の30%引きで販売したところ、実際の利益は何%だったか。
【選択肢】
A. 2% B. 5% C. 8% D. 10% E. 12%
解答と解説を見る
【解答】B. 5%
【解説】
定価=1200×1.5=1800円
販売価格=1800×0.7=1260円
利益=1260−1200=60円
利益率=60÷1200×100=5%
練習問題⑤
2種類の商品AとBを仕入れた。Aは原価400円で30個仕入れ、25%の利益を乗せた価格で販売。Bは原価500円で50個仕入れたが、10個が売れ残り、残りは20%引きで販売された。全体での利益が4880円だったとすると、商品Bの販売価格はいくらか。
【選択肢】
A. 540円 B. 550円 C. 560円 D. 570円 E. 580円
解答と解説を見る
【解答】C. 560円
【解説】
商品Aの利益:1個あたり400×0.25=100円、30個で100×30=3000円
商品Bは40個をx円で販売、10個は0.8x円で販売
Bの利益=(x−500)×40+(0.8x−500)×10
合計利益=3000+(x−500)×40+(0.8x−500)×10=4880
整理すると:3000+40x−20000+8x−5000=4880 → 48x=26880 → x=560円
よって、答えは560円
練習問題⑥
原価の40%増しで定価をつけた商品を、定価の2割引で売ったところ、損益はいくらか。(原価=5,000円)
A. 損失200円
B. 損失100円
C. 損益なし
D. 利益400円
E. 利益600円
解答と解説を見る
【解答】E
【解説】定価=5,000×1.4=7,000。販売価格=7,000×0.8=5,600。利益=5,600−5,000=600円の利益。
練習問題⑦
ある商品を10個仕入れ、1個あたり原価2,000円。定価3,000円で販売したが、2個は2割引で売った。このときの全体の利益率は?
A. 36%
B. 40%
C. 42%
D. 44%
E. 46%
解答と解説を見る
【解答】D
【解説】売上=3,000×8+2,400×2=24,000+4,800=28,800。総原価=2,000×10=20,000。利益=8,800。利益率=8,800/20,000=44%。
練習問題⑧
原価12,000円の商品を定価の80%で販売したところ、原価に対してちょうど5%の利益となった。定価はいくらか。
A. 14,400
B. 15,000
C. 15,750
D. 16,000
E. 16,200
解答と解説を見る
【解答】C
【解説】販売価格=12,000×1.05=12,600。定価xとして 0.8x=12,600 → x=15,750。
練習問題⑨
原価6,000円の商品を定価の5%引きで販売したところ、損失率が5%であった。この商品の定価は?
A. 5,800
B. 5,900
C. 6,000
D. 6,100
E. 6,200
解答と解説を見る
【解答】C
【解説】損失5% → 販売価格=6,000×0.95=5,700。定価xとして 0.95x=5,700 → x=6,000。
練習問題10
原価4,500円の商品を原価の20%増しで定価を設定し、その定価の2割引で販売した。このときの利益率は?
A. −6%
B. −5%
C. −4%
D. −3%
E. −2%
解答と解説を見る
【解答】C
【解説】定価=4,500×1.2=5,400。販売価格=5,400×0.8=4,320。損益=4,320−4,500=−180。損益率=−180/4,500=−4%。
SPI非言語の練習問題【頻出分野】「仕事算」
練習問題①
ある仕事をAが1人で行うと18日、Bが1人で行うと12日かかる。この仕事を最初にAが1人で数日行い、その後Bが1人で残りを引き継いで行ったところ、全体で仕事は14日で終わった。Aが1人で作業したのは何日か。
【選択肢】
A. 4日 B. 5日 C. 6日 D. 7日 E. 8日
解答と解説を見る
【解答】C. 6日
【解説】
全体の仕事量を18と12の最小公倍数=36とする
Aは1日で36÷18=2、Bは1日で36÷12=3の仕事量をこなせる
Aがx日作業したとすると、Bは14−x日作業
2x+3(14−x)=36 → 2x+42−3x=36 → −x=−6 → x=6
練習問題②
ある仕事をAが1人で行うと10日、Bが1人で行うと5日かかる。この仕事を2人で2日間行ったあと、Aが1人で残りを仕上げたところ、ちょうど完了した。Aが1人で作業したのは何日か。
【選択肢】
A. 1日 B. 2日 C. 3日 D. 4日 E. 5日
解答と解説を見る
【解答】D. 4日
【解説】
全体の仕事量を10と5の最小公倍数である10とすると、
Aは1日で1、Bは1日で2の仕事をこなす
2人で2日間行うと、(1+2)×2=6の仕事を完了
残りの仕事量は10−6=4
Aが1人で1日1の仕事をこなすので、4÷1=4日かかる
よってAが1人で作業したのは4日間
練習問題③
ある仕事をXとYが一緒に行うと6日、YとZが一緒に行うと3日、XとZが一緒に行うと2日で終わる。この仕事をX・Y・Zの3人で行うと、完了するのに何日か。
【選択肢】
A. 1日 B. 1.5日 C. 2日 D. 2.5日 E. 3日
解答と解説を見る
【解答】C. 2日
【解説】
まず、全体の仕事量を6と3と2の最小公倍数である6とおきます。
X+Yが6日で仕事を終えるので、1日あたりの仕事量=6÷6=1
同様に、Y+Z=6÷3=2、X+Z=6÷2=3 となります。
(X+Y)+(Y+Z)+(X+Z)=1+2+3=6
これは、X+Y+Zが2回ずつ含まれているので、
2(X+Y+Z)=6 → X+Y+Z=3
つまり、X・Y・Zの3人で1日で3の仕事ができることになります。
全体の仕事量は6なので、6÷3=2日で完了
練習問題④
ある仕事をPが1人で行うと12時間、Qが1人で行うと6時間かかる。この仕事をPとQが1時間ずつ交代しながら作業したとき、仕事は何時間で完了するか。
【選択肢】
A. 5時間 B. 6時間 C. 7時間 D. 8時間 E. 9時間
解答と解説を見る
【解答】D. 8時間
【解説】
Pは1時間で1/12、Qは1時間で1/6の仕事をする。
1サイクル(2時間)での仕事量は、1/12+1/6=1/12+2/12=3/12=1/4
つまり、2時間で全体の1/4の仕事が進む。
1÷(1/4)=4サイクル必要。1サイクルは2時間なので、4×2=8時間かかる。
したがって、仕事は8時間で完了する
練習問題⑤
ある作業をA・B・Cの3人で行う。Aは全体の作業を12時間で、Bは18時間で、Cは36時間で終えることができる。この作業を3人で協力して行うと、完了するまでに何時間かかるか。
【選択肢】
A. 6時間 B. 7時間 C. 8時間 D. 9時間 E. 10時間
解答と解説を見る
【解答】A. 6時間
【解説】
Aは1時間で1/12、Bは1/18、Cは1/36
1時間あたりの合計仕事量=1/12+1/18+1/36=(3+2+1)/36=6/36=1/6
全体の作業1を1/6ずつ行うので、1÷1/6=6時間
練習問題⑥
Aは1時間で全体の1/12、Bは1時間で全体の1/18を進める。Cも加わり、3人で一緒に作業すると6時間で終わった。Cの効率は?
A. 1/9
B. 1/12
C. 1/15
D. 1/18
E. 1/36
解答と解説を見る
【解答】E
【解説】A+B=1/12+1/18=5/36。3人の合計仕事率は 1/6(= 仕事量1 ÷ 6時間)。よって C=1/6−5/36=1/36。
練習問題⑦
Aは1人で12日、Bは1人で6日で仕事を終える。AとBが2日間一緒に作業した後、残りをCが1人で12日で終えた。Cが1人で全体を行うと何日かかるか。
A. 20日
B. 22日
C. 24日
D. 26日
E. 28日
解答と解説を見る
【解答】C
【解説】A=1/12、B=1/6。2人の1日仕事=1/12+1/6=1/4。2日で1/2が完了し、残りは1/2。これをCが12日で行ったので、Cの1日仕事量=(1/2)÷12=1/24。よってCが全体を単独で行う所要日数=1÷(1/24)=24日。
練習問題⑧
ある製品を作るのにAは1時間で20個、Bは1時間で30個作れる。2人で4時間作業すると合計何個できるか。
A. 180個
B. 190個
C. 200個
D. 210個
E. 220個
解答と解説を見る
【解答】C
【解説】(20+30)×4=200個。
練習問題⑨
定価180,000円の商品を18回の分割払いで購入する。手数料は総額の6%であり、均等割賦に含めて支払う。毎回の支払額はいくらか。
A. 10,500円
B. 10,600円
C. 10,700円
D. 10,800円
E. 10,900円
解答と解説を見る
【解答】B
【解説】総額=180,000×1.06=190,800。÷18=10,600円。
練習問題10
定価300,000円の家電を30回分割で購入する。手数料は総額の10%であり、均等割賦に含めて支払う。毎回の支払額はいくらか。
A. 10,500円
B. 10,800円
C. 11,000円
D. 11,200円
E. 11,500円
解答と解説を見る
【解答】C
【解説】総額=300,000×1.10=330,000。÷30=11,000円。
また、SPI非言語の仕事算の問題はこちらに掲載していますので、こちらからSPI仕事算のコツや解き方も含めて行ってくださいね。
SPI非言語の練習問題【頻出分野】「速度算」
練習問題①
家から目的地まで6km/hの速さで走ったところ、3km/hの速さで歩いた時に比べて8分速く着いた。このとき、家から目的地までの距離は何mか。
【選択肢】
A. 600m B. 650m C. 700m D. 750m E. 800m
解答と解説を見る
【解答】E. 800m
【解説】
距離をa[m]とおきます。
時速6km=6000m/時=100m/分、時速3km=3000m/時=50m/分
かかる時間はそれぞれ a/100 分、a/50 分
時間差は8分なので、a/50 − a/100 = 8
両辺に100をかけて、2a − a = 800 → a = 800
よって距離は800m
練習問題②
駅から学校までの距離は1.8kmである。この距離を毎朝B君は15分で歩いている。A君は同じ距離を12分で走った。このとき、A君の速さはB君より時速何km速いか。
【選択肢】
A. 0.8km/h B. 1.0km/h C. 1.5km/h D. 1.8km/h E. 2.0km/h
解答と解説を見る
【解答】D. 1.8km/h
【解説】
B君:15分=1/4時間→速さ=1.8 ÷ 1/4=7.2km/h
A君:12分=1/5時間→速さ=1.8 ÷ 1/5=9.0km/h
よって差=9.0−7.2=1.8km/h
練習問題③
A地点からB地点まで、行きは時速60kmで行き、帰りは時速40kmで戻った。このときの平均時速はいくらか。
【選択肢】
A. 48km/h B. 49km/h C. 50km/h D. 52km/h E. 54km/h
解答と解説を見る
【解答】A. 48km/h
【解説】
平均時速=2×60×40 ÷ (60+40)=4800 ÷ 100=48km/h
練習問題④
ある人が、家から駅までを時速4kmで歩いた場合は30分かかり、時速6kmで歩くと何分早く到着できるか。
【選択肢】
A. 5分 B. 8分 C. 10分 D. 12分 E. 15分
解答と解説を見る
【解答】C. 10分
【解説】
距離=時速4kmで30分(0.5時間)かかったので、4×0.5=2km
速さ6km/hで2km進むには、2 ÷ 6=1/3時間=20分
30分−20分=10分早く到着できる
練習問題⑤
長さ60mの電車が、時速54kmで走っている。踏切を通過するのに何秒かかるか。
【選択肢】
A. 2秒 B. 3秒 C. 4秒 D. 5秒 E. 6秒
解答と解説を見る
【解答】C. 4秒
【解説】
54km/h=15m/s
通過時間=60 ÷ 15=4秒
練習問題⑥
A君は9時に家を出て時速6kmで学校へ向かった。B君は9時30分に出て時速12kmで追いかけた。学校まで9kmあるとき、B君がA君に追いつくのは何時か。
A. 9時40分
B. 9時45分
C. 9時50分
D. 10時00分
E. 10時10分
解答と解説を見る
【解答】D
【解説】Aの先行距離=6×0.5=3km。速度差=12−6=6km/h。追いつきに必要な時間=3÷6=0.5時間=30分。Bの出発は9:30なので追いつきは10:00。
練習問題⑦
AとBは30km離れた地点から同時に歩き出した。Aは時速6km、Bは時速4kmで互いに向かって進む。出会うのは何時間後か。
A. 2時間
B. 2.5時間
C. 3時間
D. 3.5時間
E. 4時間
解答と解説を見る
【解答】C
【解説】合計速度=6+4=10km/h。30÷10=3時間。
練習問題⑧
A君は家から公園まで 片道5km を往復した。行きは時速10km、帰りは時速15km だった。往復の平均速度は何km/hか。
A. 11
B. 12
C. 13
D. 14
E. 15
解答と解説を見る
【解答】B
【解説】行きの時間=5 ÷ 10=0.5時間。帰りの時間=5 ÷ 15=1/3時間。総距離=5+5=10km。総時間=0.5+1/3=5/6時間。平均速度=10 ÷ (5/6)=10 × (6/5)=12km/h。
練習問題⑨
長さ200mの列車が時速72kmで走っている。長さ300mのプラットフォームを完全に通過するのに何秒かかるか。
A. 20秒
B. 25秒
C. 30秒
D. 35秒
E. 40秒
解答と解説を見る
【解答】B
【解説】必要な距離=200+300=500m。速度72km/h=20m/s。500÷20=25秒。
練習問題10
A君は8時に家を出て時速5kmで歩いた。B君は8時15分に家を出て時速10kmで同じ道を進んだ。学校まで7.5kmのとき、B君がA君に追いつくのは何時何分か。
A. 8時25分
B. 8時30分
C. 8時35分
D. 8時40分
E. 8時45分
解答と解説を見る
【解答】B
【解説】Aは15分で距離=5×0.25=1.25km先行。速度差=10−5=5km/h。追いつく時間=1.25÷5=0.25時間=15分。Bの出発が8:15なので、追いつくのは8:30。
SPI非言語の練習問題【頻出分野】「推論」
練習問題①
A~Dの4人がテストを受けた。次のことがわかっている。
- AはBより点数が高い。
- CはAより低い。
- DはAより高い。
最も高得点を取ったのは誰か?
A. A
B. B
C. C
D. D
E. AまたはD
F. BまたはC
解答と解説を見る
【解答】D
【解説】条件を整理すると、順位は D > A > B または C となるため、最高点はDである。
練習問題②
4人(P, Q, R, S)がマラソンを走った。
- QはSより早い。
- RはQより遅い。
- PはSより遅く、Rより早い。
最も遅かったのは誰か?
A. P
B. Q
C. R
D. S
E. PまたはQ
F. QまたはS
解答と解説を見る
【解答】C
【解説】条件を整理すると、順位は Q > S > P >R となるため、最も遅いのはRである。
練習問題③
4人(甲、乙、丙、丁)が総当たり戦で対戦した。
- 甲は乙に勝ったが丙に負けた。
- 丁は丙と乙に勝った。
- 丙は乙に負けた。
最も勝ち星が多いのは誰か?
A. 甲
B. 乙
C. 丙
D. 丁
E. 甲または丁
F. 乙または丙
解答と解説を見る
【解答】E
【解説】条件を整理すると、乙と丙は1勝ずつなのは確定。丁は2勝以上が確定しているが、甲と丁の結果が不明のため甲は2勝か1勝。よって正解は、甲または丁。
練習問題④
A~Dが英語テストを受けた。
- AはCより高得点。
- DはAより低い。
- CはBより高い。
最も点数が高いのは誰か?
A. A
B. B
C. C
D. D
E. AまたはC
F. BまたはD
解答と解説を見る
【解答】A
【解説】Dがどの位置に入るか確定はできないが、AがBCDよりも点数が高いことは推測されるので、最高得点はAである。
練習問題⑤
X, Y, Z, Wが短距離走に参加した。
- XはYより遅い。
- WはZより早い。
- YはWより早い。
最も早いのは誰か?
A. X
B. Y
C. Z
D. W
E. YまたはZ
F. WまたはX
解答と解説を見る
【解答】B
【解説】XがWやZとの比較がないため順位は特定できないが、YはXYZよりも早いこと早いことが推測されるため、最速はYである。
練習問題⑥
あるクラスで選択授業として、美術・書道・音楽の3科目がある。次のことがわかっている。
- 美術の人数は書道より8人多い。
- 音楽の人数は書道より4人少ない。
- クラスの人数は40人で、必ずどれか1科目を選択している。
このとき、正しいものはどれか。
A. 美術は18人
B. 書道は8人
C. 音楽は12人
D. 美術は22人
E. 書道は12人
F. 音楽は10人
解答と解説を見る
【解答】E
【解説】書道を x人とすると,美術 =x+8,音楽 =x−4。
合計より (x+8)+x+(x−4)=40⇒3x+4=40⇒x=12。
したがって,美術20人・書道12人・音楽8人。
練習問題⑦
ある学校で男子、女子、留学生の人数がいる。次のことがわかっている。
- 男子は女子より10人多い。
- 留学生は女子のちょうど半分である。
- 男子・女子・留学生を合わせると80人である。
このとき、正しいものはどれか?
A. 男子30人
B. 女子25人
C. 留学生10人
D. 男子38人
E. 女子26人
F. 留学生22人
解答と解説を見る
【解答】D
【解説】女子をxとすると、男子=x+10、留学生=x/2。
合計より (x+10)+x+(x/2)=80 → 2.5x+10=80 → 2.5x=70 → x=28。
したがって女子28人、男子38人、留学生14人。選択肢Dが正しい。
練習問題⑧
A, B, Cの3人が総あたりで1人ずつじゃんけんをした結果、次のことがわかっている。
- AはBに勝った。
- BはCに勝った。
- CはAに負けた。
勝敗に関して正しいものはどれか?
A. Aが1勝した
B. Bが2勝した
C. Cが1勝した
D. Aが全敗した
E. Bが全敗した
F. Aが最も勝ち越した
解答と解説を見る
【解答】F
【解説】AはBに勝ち、Cにも勝っている(条件1,3より)。BはCに勝ったがAに負けて1勝1敗(条件2より)。CはBに負けAにも負けて0勝(条件2,3より)。よってAが最多勝。
練習問題⑨
あるクラスでA君、B君、C君の数学の点数がある。次のことがわかっている。
- Aの点数はBより18点高い。
- Cの点数はAとBの平均より12点高い。
- A・B・Cの合計は201点である。
このとき、各自の点数として正しいものはどれか?
A. A=72点
B. B=52点
C. C=71点
D. A=78点
E. B=48点
F. C=59点
解答と解説を見る
【解答】A
【解説】Bをxとすると A=x+18,C=(A+B)/2+12=(2x+18)/2+12=x+21。
合計より (x+18)+x+(x+21)=201 ⇒ 3x+39=201 ⇒ x=54。
したがって A=72,B=54,C=75 で全条件を満たす。
練習問題10
ある商品の売上について次のことがわかっている。
- 昨年の売上は80万円であった。
- 今年の売上は昨年の135%である。
- 来年の売上は今年の70%と予測されている。
このとき、正しいものはどれか?
A. 今年の売上は135万円である
B. 来年の売上は70万円である
C. 来年の売上は昨年と同じである
D. 来年の売上は昨年より少ない
E. 来年の売上は昨年より多い
F. 正しいものはない
解答と解説を見る
【解答】D
【解説】昨年=80万円。条件2より今年=80×1.35=108万円。条件3より来年=108×0.7=75.6万円。よって「D: 来年は昨年より少ない」が正しい。
また、SPI非言語の推論の問題はこちらに掲載していますので、こちらからSPI推論のコツや解き方も含めて行ってくださいね。
更に本番形式のSPIはこちらで摸試も出来るので一度やっておく事をおすすめします。
このSPI対策摸試は無料で行えるのでWEBテスティングのSPIを極めるためにも試してみてくださいね。
SPI非言語の頻出分野を解くコツを公開!8割以上を目指そう!
SPI非言語で高得点を取るために、まず理解しておくべき重要な前提があります。それは、冒頭でもお伝えしましたがSPI非言語は「全問を完璧に解く試験ではない」という点です。
むしろ、典型的な形式を素早く見抜き、決まった考え方で処理できる問題を確実に取り切ることが、8割以上の正答率を出すための王道です。
割合や損益算、仕事算、速さ、推論といった問題は、一見すると内容がバラバラに見えますが、実際には「条件を整理し、関係性を捉える」という共通の思考プロセスが求められています。
この共通点を意識しながら、それぞれの分野の特徴とコツを理解していくことが重要です。
割合・比の問題で8割を取るための考え方
割合・比の問題は、SPI非言語の中でも特に出題頻度が高く、確実に得点源にしたい分野です。しかし同時に、「分かっているつもりでも間違えやすい」分野でもあります。
割合の問題を解く際に最も重要なのは、「何を100%として考えているのか」を常に意識することです。
売上が増えた、値段が下がった、人数の割合が変わったといった文章の中では、基準となる数値が途中で切り替わることがよくあります。
この切り替わりを見落とすと、計算自体が正しくても答えを間違えてしまいます。
文章を読んだ瞬間に数字を追いかけるのではなく、「最初の状態」「変化後の状態」「割合がかかっている対象」を整理することで、ミスを大幅に減らすことができます。
また、割合・比の問題では、無理に数字を計算し切ろうとせず、比の関係のまま考えた方が速く解けるケースも多くあります。
SPIでは答えが選択肢として用意されているため、途中式を簡略化し、関係性だけで判断できるようになると、時間効率が大きく向上します。
損益算で安定して高得点を取るためのコツ
損益算は、割合問題の応用とも言える分野であり、原価、定価、売値、利益率といった言葉が登場します。
この分野で失敗する人の多くは、言葉の定義を曖昧に理解したまま問題を解いてしまっています。
損益算で8割以上を取るためには、「原価=基準」という意識を常に持つことが非常に重要です。
利益率は原価に対する割合であることがほとんどであり、この前提を外してしまうと、計算が一気に混乱します。売値や定価に目がいきがちですが、まず原価を軸に考える癖をつけることが安定した得点につながります。
また、損益算では具体的な金額を仮定して考える方法が非常に有効です。原価を100と仮定することで、割合計算が一気にシンプルになり、計算ミスを防ぐことができます。
さらに、損益算の問題では、途中で条件が変わるケースがよくあります。値引き後の価格、複数回の売買、利益と損失の両方が登場する問題などでは、一度立ち止まって状況を整理することが重要です。
焦って計算を続けるのではなく、「今はどの状態を求めているのか」を確認することが、正答率を大きく左右します。
仕事算を得点源に変えるための思考法
仕事算は苦手意識を持つ人が多い分野ですが、考え方が分かれば非常に安定して得点できる分野でもあります。
仕事算では、複数人が作業をしたり、途中で人が増減したりしますが、最終的に完了する仕事量は常に同じです。この仕事量を1と考え、各人の作業スピードを分数で捉えることで、問題は一気に整理しやすくなります。
8割以上の正答率を出す人は、「人×時間」で考えるのではなく、「1時間あたりにどれだけ仕事が進むか」という視点で問題を見ています。誰かが1人で何日かかるかが分かれば、その人の作業効率が分かり、複数人になったときの処理もスムーズになります。
また、仕事算では、途中で条件が変わる問題が頻出します。その場合でも慌てず、「前半でどれだけ仕事が終わったか」「残りはどれくらいか」を分けて考えることが重要です。
一つの式で無理に処理しようとせず、段階的に整理することで、ミスを大幅に減らすことができます。
速さの問題で時間をかけずに正解するコツ
速さの問題は、公式そのものは非常にシンプルですが、文章が長くなることで混乱しやすい分野です。
8割以上の正答率を出すためには、速さの問題を「状況の整理問題」として捉えることが大切です。
文章を読んだら、頭の中で動きのイメージを作り、「誰が」「どの速さで」「どのくらいの時間動いているのか」を整理します。この整理ができていれば、計算自体はそれほど難しくありません。
また、速さの問題では、相対的な速さを使うと一気に解きやすくなるケースが多くあります。特に、出会いや追いつきの問題では、それぞれの速さを別々に考えるのではなく、「差」に注目することで、計算を簡略化できます。
重要なのは、公式を当てはめることよりも、「今、何が起きているのか」を理解することです。この意識を持つだけで、速さの問題に対する苦手意識は大きく減っていきます。
推論問題で8割を超えるための安定した考え方
推論問題は、SPI非言語の中でも最も差がつきやすい分野です。計算ではなく論理的な整理が求められるため、感覚で解こうとすると失敗しやすくなります。
推論問題で重要なのは、「一つずつ確実に判断する姿勢」です。条件文を読んだら、すべてを一度に理解しようとするのではなく、「この条件から確実に言えることは何か」を積み重ねていきます。
曖昧な推測や思い込みを排除し、「必ず言えるかどうか」という基準で判断することが、高正答率につながります。
選択肢が正しいかどうかは、他の選択肢と比べることで決まるのではなく、条件から論理的に導けるかどうかで決まります。
時間がかかりやすい分野ではありますが、8割を超える人は「深追いしない判断力」も身につけています。明らかに時間がかかりそうな問題は後回しにし、解ける推論を確実に取る姿勢が、全体の正答率を押し上げます。
SPI非言語で8割以上を取る人に共通する意識
SPI非言語で8割以上の正答率を出す人に共通しているのは、「考え方が型として定着している」という点です。
割合・比、損益算、仕事算、速さ、推論は、それぞれ独立した分野に見えますが、本質は「情報を整理し、関係性を捉える力」です。
正しい考え方を身につけ、焦らず、安定した判断ができる状態を作ることが、SPI非言語で8割以上を達成するための最も確実な方法です。
スマホでこのページを見ている方限定でお伝えしたいのが、今まさに出題されているSPIの問題が出ると評判の「Lognavi」というアプリです。
MBTI顔負けの性格診断も出来て、あなたの市場価値まで企業側に伝わって超大手優良企業からのオファーももらえちゃうから一石二鳥です!

下記のURLからアプリインストール画面に飛べるので、今のうちにインストールして初回起動だけでもしておきましょう!
自分のSPIの出来を今のうちに判断した方が正確で対策しやすいですよ。
アプリインストールはこちらから⇒https://lognavi.com/
※インストール後の初回起動はお早めに
\ 先ずはインストール /
ESや企業研究でSPIに時間を割く暇がないと思うので、今選考で出題されているSPIの練習が無料でできるSPIの無料問題集をやっておいてください。
無料でダウンロードできるので、SPIに時間をかけたくない場合は使ってみてください。
▼25卒に大人気でした▼
参考書や問題集と違って問題が最新版にアップデートされるので、今どのような問題が出題されているのか、頻出問題ばかりなのでチェックするためにも利用すると良いでしょう。
とくにWEBテストは出題される問題の難易度もまばらなので、長文や推論などが苦手な学生ほど使っておく事をおすすめします。
一応リンク貼っておくので、自由に使ってみてください。
SPI問題集公式⇒https://careerpark.jp/
こちらの記事も参考にしてくださいね。
SPI非言語の練習問題で推論や頻出分野を解説つきで無料公開まとめ
SPI非言語の練習問題や推論や頻出分野を解くコツなどは参考になりましたでしょうか。
SPIの非言語は手こずる学生が非常に多く、ここで躓いてしまって面接まで進めない事が非常に勿体ないです。
本来であればSPIで出題される非言語くらい解ける力はあるのに、練習を行ってこなかったせいで出題形式に慣れる事ができず、早々に時間切れになってしまうなど、あるあるです。
練習を行えば行うだけ良い結果が出る可能性は高まるので、ここをどれだけ追い込めるかでライバルに差がつきますよ。
- 今選考で出題されている問題が出る!「Lognavi」
「Lognavi」は今企業の選考で出題されているSPIの問題が出ると評判のアプリで、SPIの偏差値も出せるので、自分のレベルを知るためにも利用する価値があるアプリです。
Lognavi公式はこちら⇒https://lognavi.com/
- 最新のSPIを何度でも練習できる!「キャリアパーク」
「キャリアパーク」のSPIパーフェクト問題集は最新のSPIの問題が200問あり、解答や解説もついているので非常に学びになる無料の問題集です。
SPIの解答集つき問題集公式⇒https://careerpark.jp/
- 志望企業のSPIを通過できるかSPI判定もできる「キミスカ」
「キミスカ」はあなたが志望する企業のSPIのボーダーを突破できるか判定してくれる機能もあるサービスです。
キミスカ公式はこちら⇒https://kimisuka.com/
















コメント